Table of Contents
Triplet Loss with Keras and TensorFlow
In today’s tutorial, we will try to understand the formulation of the triplet loss and build our Siamese Network Model in Keras and TensorFlow, which will be used to develop our Face Recognition application.
In the previous tutorial of this series, we built the dataset and data pipeline for our Siamese Network based Face Recognition application. Specifically, we looked at an overview of triplet loss and discussed what kind of data samples are required to train our model with the triplet loss. We also used Keras and TensorFlow to develop modules that allow us to process our dataset and generate triplet data samples that can be used to train our model.
Furthermore, we discussed and implemented face detection and cropping, which form an important part of the data pipeline and allow our face recognition model to effectively make predictions based on facial features.
In this tutorial, we will dive deeper into the definition of the triplet and discuss its mathematical formulation in detail. Furthermore, we will build our Siamese Network model and write our own triplet loss function, which will form the basis for our face recognition application and later be used to train our face recognition application.
This lesson is the 3rd of a 5-part series on Siamese Networks and their application in face recognition:
- Face Recognition with Siamese Networks, Keras, and TensorFlow
- Building a Dataset for Triplet Loss with Keras and TensorFlow
- Triplet Loss with Keras and TensorFlow (this tutorial)
- Training and Making Predictions with Siamese Networks and Triplet Loss
- Evaluating Siamese Network Accuracy (F1-Score, Precision, and Recall) with Keras and TensorFlow
To learn how to write your own triplet loss with Keras and TensorFlow, just keep reading.
Triplet Loss with Keras and TensorFlow
In the first part of this series, we discussed the basic formulation of a contrastive loss and how it can be used to learn a distance measure based on similarity. Furthermore, in the previous tutorial, we looked at the type of data samples required to train our model with triplet loss and discussed the anchor, positive, and negative data samples.
The triplet loss uses these samples to learn an embedding space where samples from the same person or class lie close to each other and samples from different classes or persons lie farther apart. It is based on the idea that the distance between the representation of the anchor and negative samples (which belong to different people) should be at least a “margin” distance more than the distance between the anchor and positive samples. Here, “margin” is a hyperparameter similar to the one we discussed in the definition of pairwise contrastive loss in the first part of this series.
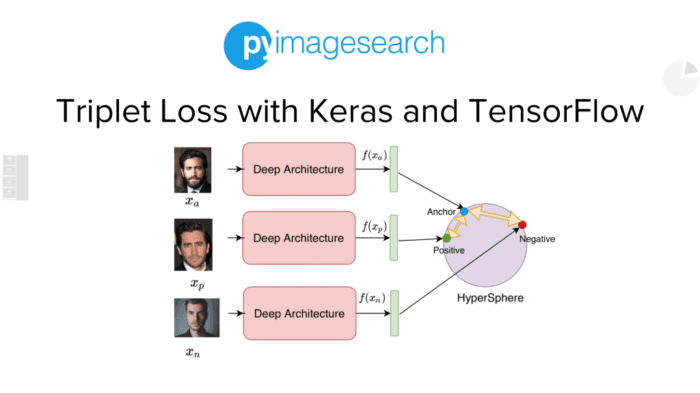
Let us try to delve deeper and understand this with an example. Figure 1 shows a typical pipeline for training a Siamese Network based Face Recognition model with Triplet Loss.
Suppose we have a database of faces, and we draw a triplet sample consisting of an anchor image , positive image
, and negative image
. Remember, as discussed in the previous tutorial, that the anchor and positive images are different instances of faces of the same person, and the anchor and negative images come from different people. The three images are passed through our deep network (denoted as Deep Architecture in the figure) to get the corresponding representations in the embedding space, that is,
,
, and
. Usually, each of these representations is then normalized to have a unit norm. In other words, this means that they will lie on a hypersphere with a radius of 1 in the embedding space since each has a norm equal to 1 (as shown in Figure 1).
Let us now discuss how we use the triplet loss to train this network and understand its mathematical formulation.
The equation above shows the formulation of the triplet loss we will use to train our Siamese Network. Notice that here refers to the square of the L2 norm of
, which is simply the square of the Euclidean distance between our representations
and
. Let us refer to this as
.
Similarly, is the square of the Euclidean distance between our representations
and
, which we refer to as
. Furthermore, the
parameter refers to the margin distance.
After simplification, our final equation for triplet loss is as follows.
Notice that the minimum value of this expression is 0, and it occurs when the term . Rearranging the terms, we notice that this implies that this loss is minimized when
In other words, optimizing our model to minimize the triplet loss ensures that the distance between our anchor and negative representations is at least margin = higher than the distance between our anchor and positive representations. This allows us to learn an embedding space where our anchor and positive representations are close and the anchor and negative representations are farther apart.
Now that we have discussed the mathematical formulation of the triplet loss, let us look at the internal structure of the deep network (referred to as Deep Architecture in Figure 1) that we will be using for our face recognition application.
Figure 2 shows the internal structure of the Deep Architecture block, which we refer to as the Embedding Module in the code for this tutorial. The function of the Embedding Module is to take our anchor, positive, and negative samples in the image space and map them to d-dimensional representations in the embedding space, as shown.
The embedding module is composed of a backbone network and a trainable module. This tutorial uses the ResNet-50 (without the final head) as the backbone feature extractor. Note that the backbone is initialized with ImageNet weights, and its weights are frozen. Furthermore, we additionally use a lightweight trainable module composed of fully connected layers to get the final d-dimensional representation for our inputs. Notice that this setup allows us to use the feature extraction capabilities of the ResNet-50 backbone without having to train such a big network. Furthermore, the trainable module gives our embedding module the flexibility to learn the appropriate function for the task without training numerous parameters.
Now that we have discussed an overview of our Siamese Model pipeline, the formulation of the triplet loss, and the internal structure of our modules, let us code our Siamese Model with Keras and TensorFlow.
Configuring Your Development Environment
To follow this guide, you need to have the TensorFlow and OpenCV libraries installed on your system.
Luckily, both TensorFlow and OpenCV are pip-installable:
$ pip install tensorflow $ pip install opencv-contrib-python
If you need help configuring your development environment for OpenCV, we highly recommend that you read our pip install OpenCV guide — it will have you up and running in a matter of minutes.
Having Problems Configuring Your Development Environment?
All that said, are you:
- Short on time?
- Learning on your employer’s administratively locked system?
- Wanting to skip the hassle of fighting with the command line, package managers, and virtual environments?
- Ready to run the code right now on your Windows, macOS, or Linux system?
Then join PyImageSearch University today!
Gain access to Jupyter Notebooks for this tutorial and other PyImageSearch guides that are pre-configured to run on Google Colab’s ecosystem right in your web browser! No installation required.
And best of all, these Jupyter Notebooks will run on Windows, macOS, and Linux!
Project Structure
We first need to review our project directory structure.
Start by accessing the “Downloads” section of this tutorial to retrieve the source code and example images.
├── crop_faces.py ├── face_crop_model │ ├── deploy.prototxt.txt │ └── res10_300x300_ssd_iter_140000.caffemodel ├── inference.py ├── pyimagesearch │ ├── config.py │ ├── dataset.py │ └── model.py └── train.py
In the previous tutorial, we discussed the directory structure for our Siamese Network based Face Recognition application in detail. Furthermore, we presented a step-by-step walkthrough of our config.py, dataset.py, and crop_faces.py files, which allow us to process input data and build the data pipeline.
In this tutorial, we will discuss the model.py file from the pyimagesearch folder, which implements the code for our Siamese Network Model and triplet loss function.
Implementing Siamese Model and Triplet Loss
Now that we have discussed the concepts required to build our Siamese Model, let’s dive into the code and implement the triplet loss and Siamese network in Keras and TensorFlow.
We open our model.py file from the pyimagesearch folder and get started.
# import the necessary packages
from tensorflow.keras.applications import resnet
from tensorflow.keras import layers
from tensorflow import keras
import tensorflow as tf
def get_embedding_module(imageSize):
# construct the input layer and pass the inputs through a
# pre-processing layer
inputs = keras.Input(imageSize + (3,))
x = resnet.preprocess_input(inputs)
# fetch the pre-trained resnet 50 model and freeze the weights
baseCnn = resnet.ResNet50(weights="imagenet", include_top=False)
baseCnn.trainable=False
# pass the pre-processed inputs through the base cnn and get the
# extracted features from the inputs
extractedFeatures = baseCnn(x)
# pass the extracted features through a number of trainable layers
x = layers.GlobalAveragePooling2D()(extractedFeatures)
x = layers.Dense(units=1024, activation="relu")(x)
x = layers.Dropout(0.2)(x)
x = layers.BatchNormalization()(x)
x = layers.Dense(units=512, activation="relu")(x)
x = layers.Dropout(0.2)(x)
x = layers.BatchNormalization()(x)
x = layers.Dense(units=256, activation="relu")(x)
x = layers.Dropout(0.2)(x)
outputs = layers.Dense(units=128)(x)
# build the embedding model and return it
embedding = keras.Model(inputs, outputs, name="embedding")
return embedding
We start by importing the necessary packages and modules to build our Siamese Model on Lines 2-5.
On Lines 7-35, we develop the embedding module of our Siamese model that we discussed above. This module takes as input the imageSize (i.e., height and width of the input image) as shown on Line 7.
We start by defining the input layer using the keras.Input function, as shown on Line 10. This layer takes as input the imageSize (i.e., its height and width) along the number of channels (i.e., (3,)) of our input image. Then on Line 11, we pass our inputs through the preprocessing layer of our backbone reset network.
On Line 14, we initialize our ResNet50 backbone model and load the pre-trained ImageNet weights using the weights="imagenet" argument. Furthermore, we use include_top=False since we only need the backbone network without the final fully connected layers. On Line 15, we set baseCnn.trainable=False to freeze the weights of our resnet backbone.
On Line 19, we pass our input x through our baseCnn and store the output features in extractedFeatures as shown. Next, we pass the extracted features through our trainable layers on Lines 22-30. We first consolidate the extractedFeatures using the layers.GlobalAveragePooling2D() layer (Line 22) and then pass it through a 1024-dimensional fully connected layer with relu activation using layers.Dense(units=1024, activation="relu") (Line 23). Next, we use the Dropout regularization layer on Line 24. Then, we use a series of BatchNormalization → Dense → Dropout layers (Lines 25-30) and finally pass our processed output x through the final 128-dimensional fully connected layer on Line 31.
Finally, we build the embedding model using the keras.Model function with our computed inputs and outputs as the input and output to our model (Line 34). We then return our embedding model on Line 35.
def get_siamese_network(imageSize, embeddingModel):
# build the anchor, positive and negative input layer
anchorInput = keras.Input(name="anchor", shape=imageSize + (3,))
positiveInput = keras.Input(name="positive", shape=imageSize + (3,))
negativeInput = keras.Input(name="negative", shape=imageSize + (3,))
# embed the anchor, positive and negative images
anchorEmbedding = embeddingModel(anchorInput)
positiveEmbedding = embeddingModel(positiveInput)
negativeEmbedding = embeddingModel(negativeInput)
# build the siamese network and return it
siamese_network = keras.Model(
inputs=[anchorInput, positiveInput, negativeInput],
outputs=[anchorEmbedding, positiveEmbedding, negativeEmbedding]
)
return siamese_network
Now we build our get_siamese_network function, which takes as input imageSize and embeddingModel and returns our siamese_network (Lines 37-53).
On Lines 39-41, we build an input layer for each anchor, positive, and negative samples using the keras.Input layer. Next, on Lines 44-46, we use the embeddingModel to embed our anchorInput, positiveInput, and negativeInput.
Finally, on Lines 49-52, we build our Siamese network model with [anchorInput, positiveInput, negativeInput] as the input and [anchorEmbedding, positiveEmbedding, negativeEmbedding] as the output. We return our siamese_network on Line 53.
class SiameseModel(keras.Model):
def __init__(self, siameseNetwork, margin, lossTracker):
super().__init__()
self.siameseNetwork = siameseNetwork
self.margin = margin
self.lossTracker = lossTracker
def _compute_distance(self, inputs):
(anchor, positive, negative) = inputs
# embed the images using the siamese network
embeddings = self.siameseNetwork((anchor, positive, negative))
anchorEmbedding = embeddings[0]
positiveEmbedding = embeddings[1]
negativeEmbedding = embeddings[2]
# calculate the anchor to positive and negative distance
apDistance = tf.reduce_sum(
tf.square(anchorEmbedding - positiveEmbedding), axis=-1
)
anDistance = tf.reduce_sum(
tf.square(anchorEmbedding - negativeEmbedding), axis=-1
)
# return the distances
return (apDistance, anDistance)
def _compute_loss(self, apDistance, anDistance):
loss = apDistance - anDistance
loss = tf.maximum(loss + self.margin, 0.0)
return loss
def call(self, inputs):
# compute the distance between the anchor and positive,
# negative images
(apDistance, anDistance) = self._compute_distance(inputs)
return (apDistance, anDistance)
def train_step(self, inputs):
with tf.GradientTape() as tape:
# compute the distance between the anchor and positive,
# negative images
(apDistance, anDistance) = self._compute_distance(inputs)
# calculate the loss of the siamese network
loss = self._compute_loss(apDistance, anDistance)
# compute the gradients and optimize the model
gradients = tape.gradient(
loss,
self.siameseNetwork.trainable_variables)
self.optimizer.apply_gradients(
zip(gradients, self.siameseNetwork.trainable_variables)
)
# update the metrics and return the loss
self.lossTracker.update_state(loss)
return {"loss": self.lossTracker.result()}
def test_step(self, inputs):
# compute the distance between the anchor and positive,
# negative images
(apDistance, anDistance) = self._compute_distance(inputs)
# calculate the loss of the siamese network
loss = self._compute_loss(apDistance, anDistance)
# update the metrics and return the loss
self.lossTracker.update_state(loss)
return {"loss": self.lossTracker.result()}
@property
def metrics(self):
return [self.lossTracker]
Now, we define our SiameseModel class which will allow us to implement and apply the triplet loss function during the training and test steps of our Face Recognition Application (Lines 55-127).
We start by defining the _init_ function, which takes as arguments the siameseNetwork, the margin, and the lossTracker (which allows us to log and track the losses during training), as shown on Line 56. Then, on Lines 58-60, we assign these arguments to create the self.siameseNetwork, self.margin, and self.lossTracker attributes of the class.
Now we will discuss the _compute_distance function (Lines 62-79), which takes the inputs (i.e., (anchor, positive, negative) samples) and computes the distance between the anchor and positive sample (i.e., apDistance) and the anchor and negative sample (i.e., anDistance).
We start by unpacking our inputs (i.e., anchor, positive, and negative samples) on Line 63. Next, we embed them by passing them through our self.siameseNetwork and storing the outputs in embeddings, as shown on Line 65.
On Lines 66-69, we unpack the embeddings of our anchor sample (i.e., anchorEmbedding), positive sample (i.e., positiveEmbedding), and negative sample (i.e., negativeEmbedding).
Next, we compute the square of the Euclidean distance between the anchor and positive embedding (i.e., apDistance) on Lines 71 and 72. Similarly, we compute the distance between the anchor and negative embedding (i.e., anDistance) on Lines 74-76). Finally, we return the distances (i.e., (apDistance, anDistance)) on Line 79.
Now that we have computed the distances between our embeddings, let us write a function to compute our triplet loss. We define the _compute_loss function (Lines 81-84), which takes as input the distance between the anchor and positive (i.e., apDistance) and anchor and negative embeddings (i.e., anDistance).
On Line 81, we compute the difference between apDistance and anDistance, and on Line 83, we implement our triplet loss equation which we discussed before.
Finally, we return our computed loss on Line 84.
On Lines 86-90, we define our call function that takes the inputs and uses the self._compute_distance function to compute apDistance and anDistance (Line 89) and finally returns these distances on Line 90.
Finally, let us discuss how the triplet loss is applied during our model’s training and test phase.
We discuss the train_step function defined on Lines 92-111, which takes the inputs as arguments, as shown on Line 92. During the training phase, we want to keep track of the gradients during loss computation to use them during backpropagation. Thus, we work inside with tf.GradientTape() as tape: block, as shown on Line 93.
We first compute the distance between the anchor and positive (i.e., apDistance) and anchor and negative embeddings (i.e., anDistance) using the self._compute_distance function on Line 96. Then we use the self._compute_loss function defined above to compute our triplet loss and store it as loss as shown on Line 99.
Next, on Lines 102-104, we compute the gradients of our loss w.r.t. the trainable parameters of our Siamese Network (i.e., self.siameseNetwork.trainable_variables) as shown. We then update the weights to optimize the model using self.optimizer.apply_gradients, which takes the gradients and the corresponding trainable variables as shown on Lines 105-107. Finally, we use the computed loss to update the loss metric and return the loss on Lines 110 and 111.
Now that we have discussed the training step, let us further discuss the test_step function (Lines 113-123). Note that this function will be very similar to the train_step function, with the only difference being that the gradients will not be tracked or computed, and there will be loss optimization since we are in the test or inference phase.
Similar to the train_step function, the test_step function also takes the inputs as the argument, as shown on Line 113. Next, we compute the apDistance and anDistance on Line 116 and compute the triplet loss on Line 119 as we did previously in the training step. Finally, we use the computed loss to update the loss metric and return the loss on Lines 122 and 123.
Ultimately, we define our metrics function that simply returns our self.lossTracker, which keeps track of our metrics.
This completes the code walkthrough to build our Siamese model and triplet loss function.
What's next? We recommend PyImageSearch University.
86+ total classes • 115+ hours hours of on-demand code walkthrough videos • Last updated: July 2025
★★★★★ 4.84 (128 Ratings) • 16,000+ Students Enrolled
I strongly believe that if you had the right teacher you could master computer vision and deep learning.
Do you think learning computer vision and deep learning has to be time-consuming, overwhelming, and complicated? Or has to involve complex mathematics and equations? Or requires a degree in computer science?
That’s not the case.
All you need to master computer vision and deep learning is for someone to explain things to you in simple, intuitive terms. And that’s exactly what I do. My mission is to change education and how complex Artificial Intelligence topics are taught.
If you're serious about learning computer vision, your next stop should be PyImageSearch University, the most comprehensive computer vision, deep learning, and OpenCV course online today. Here you’ll learn how to successfully and confidently apply computer vision to your work, research, and projects. Join me in computer vision mastery.
Inside PyImageSearch University you'll find:
- ✓ 86+ courses on essential computer vision, deep learning, and OpenCV topics
- ✓ 86 Certificates of Completion
- ✓ 115+ hours hours of on-demand video
- ✓ Brand new courses released regularly, ensuring you can keep up with state-of-the-art techniques
- ✓ Pre-configured Jupyter Notebooks in Google Colab
- ✓ Run all code examples in your web browser — works on Windows, macOS, and Linux (no dev environment configuration required!)
- ✓ Access to centralized code repos for all 540+ tutorials on PyImageSearch
- ✓ Easy one-click downloads for code, datasets, pre-trained models, etc.
- ✓ Access on mobile, laptop, desktop, etc.
Summary
In this tutorial, we discussed building a Siamese Network based Face Recognition Model using Keras and TensorFlow. Specifically, we tried to understand the details of the triplet loss and closely looked at a typical pipeline for training our Siamese Network Model with Triplet Loss.
Furthermore, we discussed the mathematical formulation of the triplet loss. We saw how it enforces the anchor and positive representations to be closer to each other and the anchor and negative representations to be farther apart. Additionally, we discussed the internal structure of the embedding module, which allows us to efficiently map our faces from the image space to the embedding space.
In the upcoming tutorials of this series, we will see how we can train our Siamese Network and make predictions using it in real-time.
Credits
This post is inspired by the amazing National Programme on Technology Enhanced Learning (NPTEL) Deep Learning for Computer Vision Course, which the author contributed to while working at IIT Hyderabad.
Citation Information
Chandhok, S. “Triplet Loss with Keras and TensorFlow,” PyImageSearch, P. Chugh, A. R. Gosthipaty, S. Huot, K. Kidriavsteva, R. Raha, and A. Thanki, eds., 2023, https://pyimg.co/2try0
@incollection{Chandhok_2023_TLwK+TF,
author = {Shivam Chandhok},
title = {Triplet Loss with {Keras and TensorFlow}},
booktitle = {PyImageSearch},
editor = {Puneet Chugh and Aritra Roy Gosthipaty and Susan Huot and Kseniia Kidriavsteva and Ritwik Raha and Abhishek Thanki},
year = {2023},
url = {https://pyimg.co/2try0},
}

Unleash the potential of computer vision with Roboflow - Free!
- Step into the realm of the future by signing up or logging into your Roboflow account. Unlock a wealth of innovative dataset libraries and revolutionize your computer vision operations.
- Jumpstart your journey by choosing from our broad array of datasets, or benefit from PyimageSearch’s comprehensive library, crafted to cater to a wide range of requirements.
- Transfer your data to Roboflow in any of the 40+ compatible formats. Leverage cutting-edge model architectures for training, and deploy seamlessly across diverse platforms, including API, NVIDIA, browser, iOS, and beyond. Integrate our platform effortlessly with your applications or your favorite third-party tools.
- Equip yourself with the ability to train a potent computer vision model in a mere afternoon. With a few images, you can import data from any source via API, annotate images using our superior cloud-hosted tool, kickstart model training with a single click, and deploy the model via a hosted API endpoint. Tailor your process by opting for a code-centric approach, leveraging our intuitive, cloud-based UI, or combining both to fit your unique needs.
- Embark on your journey today with absolutely no credit card required. Step into the future with Roboflow.
To download the source code to this post (and be notified when future tutorials are published here on PyImageSearch), simply enter your email address in the form below!

Download the Source Code and FREE 17-page Resource Guide
Enter your email address below to get a .zip of the code and a FREE 17-page Resource Guide on Computer Vision, OpenCV, and Deep Learning. Inside you'll find my hand-picked tutorials, books, courses, and libraries to help you master CV and DL!


Comment section
Hey, Adrian Rosebrock here, author and creator of PyImageSearch. While I love hearing from readers, a couple years ago I made the tough decision to no longer offer 1:1 help over blog post comments.
At the time I was receiving 200+ emails per day and another 100+ blog post comments. I simply did not have the time to moderate and respond to them all, and the sheer volume of requests was taking a toll on me.
Instead, my goal is to do the most good for the computer vision, deep learning, and OpenCV community at large by focusing my time on authoring high-quality blog posts, tutorials, and books/courses.
If you need help learning computer vision and deep learning, I suggest you refer to my full catalog of books and courses — they have helped tens of thousands of developers, students, and researchers just like yourself learn Computer Vision, Deep Learning, and OpenCV.
Click here to browse my full catalog.