Post Training Qwen3 for Math Reasoning Using GRPO

---

---

Post Training Qwen3 for Math Reasoning Using GRPO

Pre-training a language model is like teaching someone to read by showing them millions of books. Sure, they’ll learn the patterns of language, understand grammar, and even pick up some facts along the way. But can they follow specific instructions? Can they reason through a multi-step math problem? Can they align their responses with what humans actually want to hear? Not quite.

This is where post-training techniques come into play. These approaches transform foundation models from general-purpose text generators into specialized systems capable of complex reasoning.

Post-training optimization encompasses a spectrum of techniques, including supervised fine-tuning (SFT), instruction tuning, reinforcement learning from human feedback (RLHF), and advanced policy optimization methods. The significance of this phase cannot be overstated, as evidenced by recent breakthroughs in reasoning-capable models (e.g., OpenAI’s o1 series and DeepSeek’s R1), which demonstrate that sophisticated post-training techniques can dramatically enhance multi-step reasoning and mathematical problem-solving capabilities.

The mathematical reasoning domain presents unique challenges that traditional post-training approaches struggle to address effectively. Mathematical problem-solving requires not only accurate fact retrieval but also the ability to perform multi-step logical inference, maintain consistency across extended reasoning chains, and apply abstract principles to novel problem configurations.

In this blog post, we will understand and apply Group Relative Policy Optimization (GRPO) — one of the main pillars of DeepSeek R1’s success — to post-train small language models (e.g., Qwen3) for mathematical reasoning.

This lesson is the last of a 2-part series on Preference Optimization:

1. Fine Tuning SmolVLM for Human Alignment Using Direct Preference Optimization
2. Post Training Qwen3 for Math Reasoning Using GRPO (this tutorial)

To learn how to post-train Qwen3 for Mathematical Reasoning using GRPO, just keep reading.

---

Group Relative Policy Optimization (GRPO)

---

Challenges with Proximal Policy Optimization (PPO)?

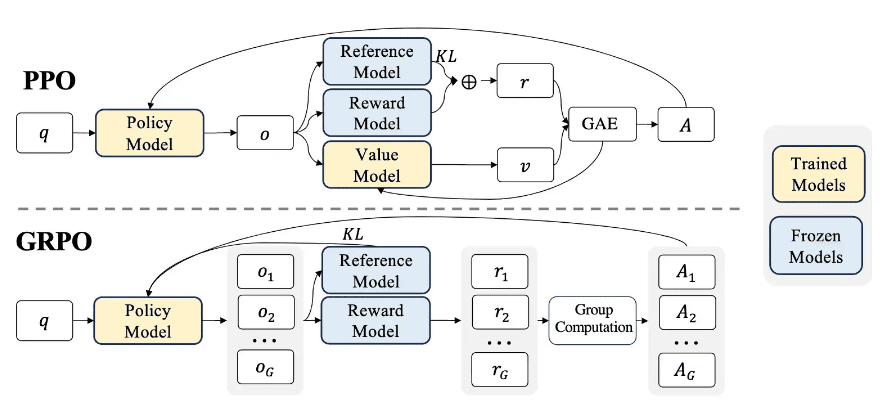
Proximal Policy Optimization (PPO) has long been considered the gold standard for reinforcement learning in large language model training, particularly in RLHF pipelines (Figure 1). However, despite its widespread adoption, PPO presents several fundamental challenges that become particularly pronounced when applied to language model training and complex reasoning tasks.

---

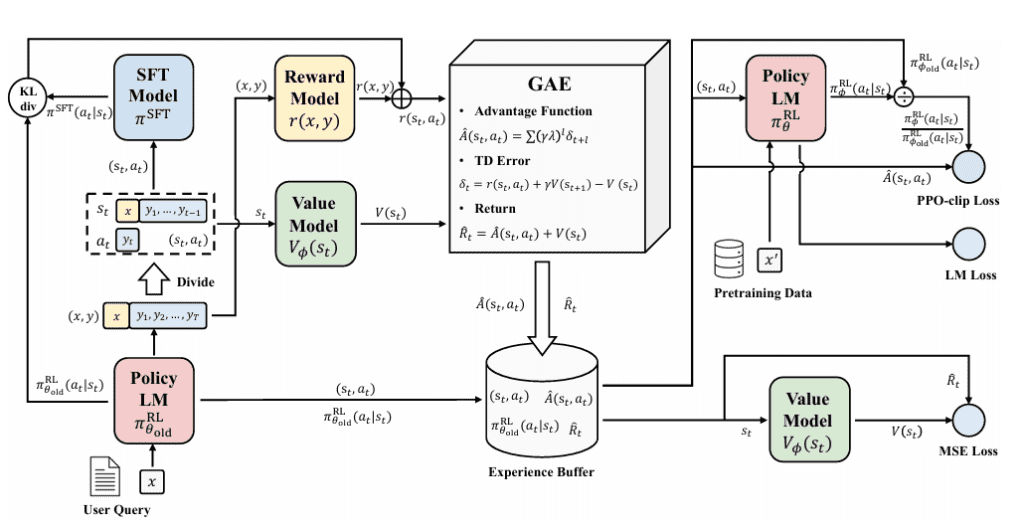
Computational Overhead and Memory Requirements

One of the most significant limitations of PPO is its substantial computational overhead and memory requirements. PPO necessitates maintaining multiple models simultaneously during training: the policy network (actor), the value function network (critic), a reference policy, and often a reward model (Figure 2). This multi-model architecture creates several problems:

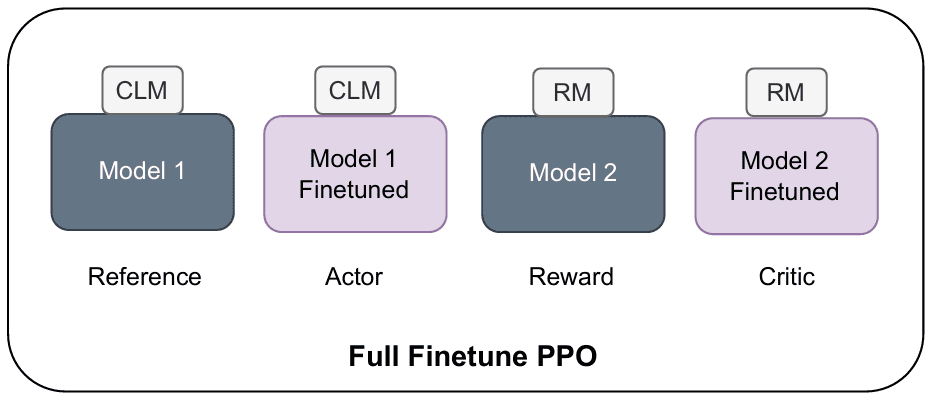
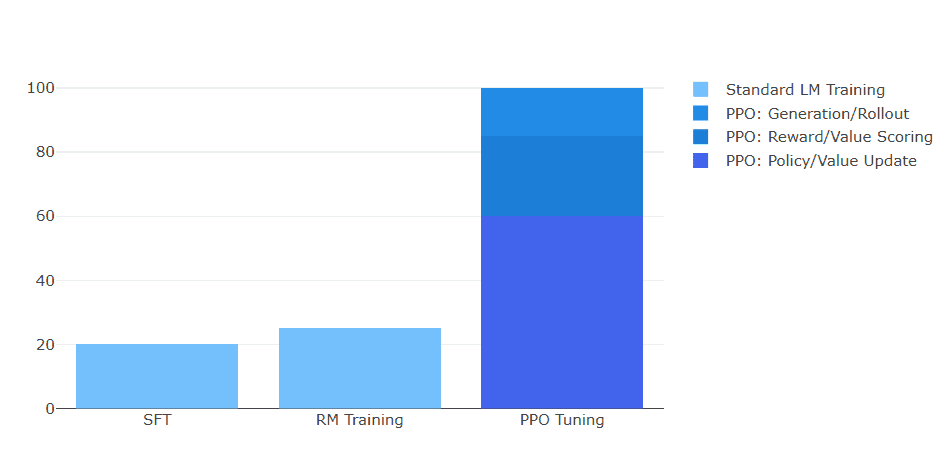
The memory requirements for PPO can be over three times that of supervised fine-tuning, making it infeasible for many practitioners with limited computational resources (Figure 3). The need to load and maintain multiple models in memory during training creates significant bottlenecks, especially when working with large language models that already push the boundaries of available GPU memory.

---

Value Function Instability and Representation Collapse

PPO’s reliance on a separate value function network introduces additional complexity and potential points of failure. The value network must accurately estimate the expected future rewards for given states, but this estimation becomes increasingly difficult in the non-stationary environment created by the continuously updating policy.

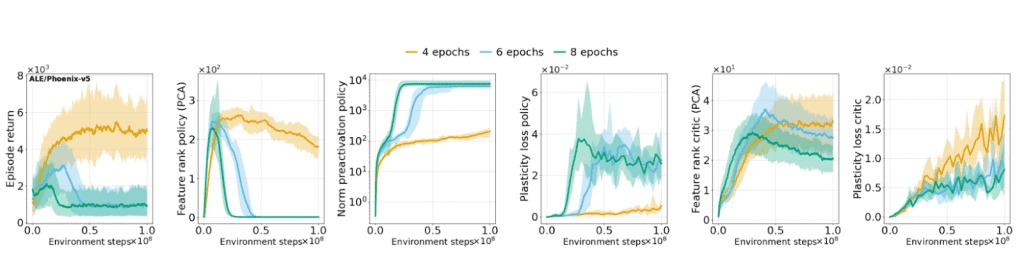
Research has revealed that PPO agents suffer from feature rank deterioration and loss of plasticity over time, leading to what researchers term “representation collapse” (Figure 4). This phenomenon manifests as a decrease in the rank of learned representations, which correlates with the value network’s inability to continue learning and adapting to new observations. The collapse is particularly pronounced in longer training runs and can ultimately drive the actor’s performance to collapse regardless of the critic’s performance.

---

Hyperparameter Sensitivity and Training Instability

PPO is notoriously sensitive to hyperparameter choices, requiring careful tuning of learning rates, clipping parameters, value function coefficients, and entropy bonuses. Small changes in these parameters can lead to drastically different training outcomes, making PPO difficult to deploy reliably across different tasks and model scales (Figure 5).

The algorithm’s training dynamics can be unstable, particularly in long-chain-of-thought reasoning scenarios that are crucial for mathematical reasoning tasks. PPO can struggle with the temporal credit assignment problem when rewards are sparse and delayed, as is often the case in multi-step reasoning problems.

---

Bias in Value Function Estimation

The value function in PPO can introduce bias in advantage estimation, particularly when the value network fails to represent the true value of states accurately. This bias can accumulate over training iterations, leading to suboptimal policy updates and potentially causing the model to learn incorrect associations between actions and rewards.

These fundamental limitations of PPO have motivated researchers to develop alternative approaches that can maintain the benefits of reinforcement learning while addressing these computational and stability concerns. Group Relative Policy Optimization (GRPO) represents one such advancement, designed specifically to overcome many of these limitations while providing efficient and stable training for complex reasoning tasks.

---

GRPO Objective Function

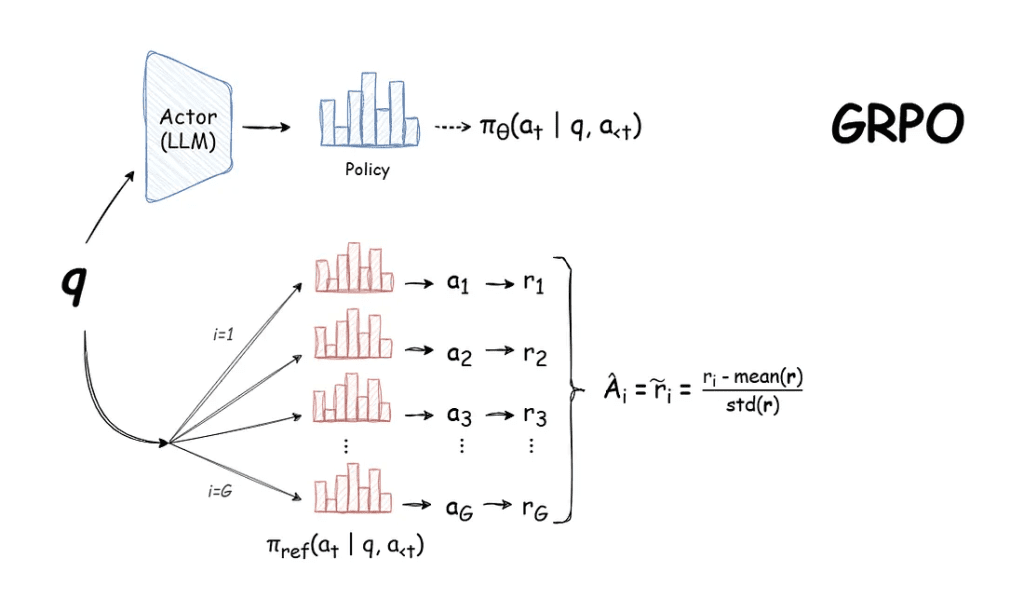
Group Relative Policy Optimization (GRPO) represents a fundamental departure from traditional policy optimization methods by eliminating the need for a separate value function while maintaining stable and efficient training dynamics (Figure 6). The mathematical foundation of GRPO is built on the principle of group-relative advantage estimation, which provides both computational efficiency and variance reduction.

---

Core GRPO Objective

The GRPO objective function can be formally expressed as (Figure 7):

where:

• : represents the input prompt or question
• : represents a group of outputs/completions generated for the same prompt
• : is the clipped advantage function
• : is the KL divergence penalty term
• : is the regularization coefficient

---

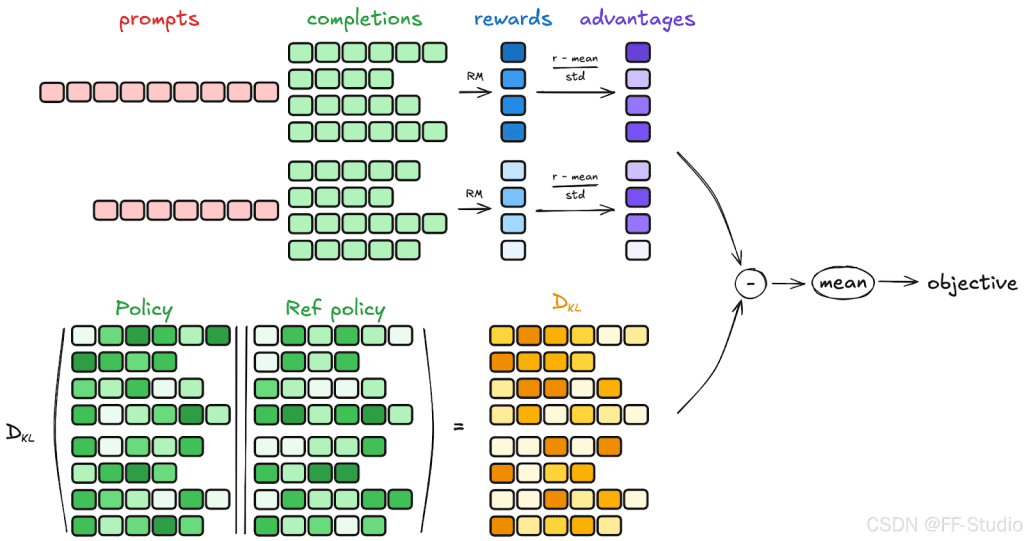
Group Relative Advantage Estimation

The key innovation of GRPO lies in its advantage estimation mechanism. Instead of relying on a learned value function (e.g., PPO), GRPO computes advantages relative to the group of sampled outputs (Figure 8):

where:

• : is the reward for output
• : is the group mean reward
• : is the group standard deviation

This normalization serves multiple purposes. It provides a natural baseline by comparing each output against its peers, reduces variance by localizing comparisons within each group, and eliminates the need for a separate value function approximator.

---

Clipped Surrogate Objective

Following PPO’s approach, GRPO employs a clipped surrogate objective to maintain training stability:

where constrains to the range , preventing excessively large policy updates that could destabilize training.

---

KL Divergence Regularization

The KL (Kullback-Leibler) divergence term in the GRPO objective serves to keep the updated policy close to a reference policy , typically the initial supervised fine-tuned model:

This regularization term is particularly important in language model training to prevent catastrophic forgetting of the model’s pre-trained capabilities.

---

Why GRPO Excels in Mathematical Reasoning

Group Relative Policy Optimization (GRPO) has rapidly established itself as a leading fine-tuning approach for mathematical reasoning in large language models, owing to several structural features that make it especially well-suited to this domain.

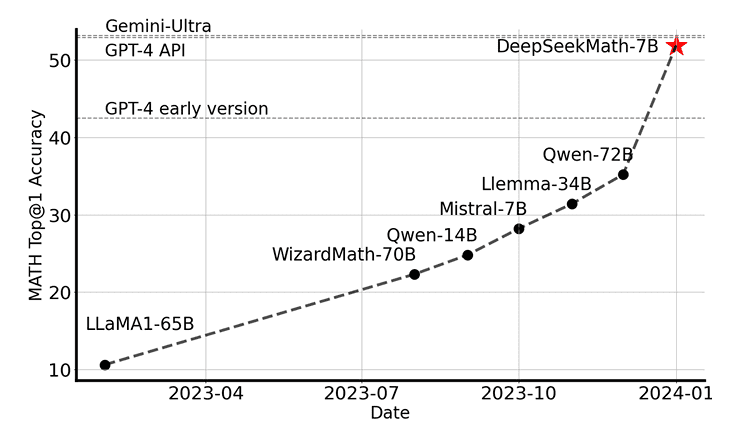
Recent large-scale studies (e.g., those involving the DeepSeekMath and DeepSeek-R1 models) demonstrate that swapping PPO for GRPO in RLHF pipelines yields significant improvements on mathematical reasoning benchmarks (e.g., GSM8K, MATH datasets).

For example, DeepSeekMath training with GRPO outperformed PPO-based methods on math reasoning accuracy while reducing compute costs (Figure 9).

---

Intrinsic Support for Verifiable Rewards

Mathematics problem-solving offers an unusually clear and verifiable reward mechanism: answers are either correct or incorrect, and partial credit can be precisely defined. GRPO capitalizes on this by scoring multiple solutions generated for each problem using a well-defined reward model — often simply marking correct steps or final answers. This direct and reliable reward assignment enhances the signal-to-noise ratio of model updates, as each policy improvement step is based on unambiguous performance feedback.

In contrast, open-ended tasks (e.g., creative writing or dialogue) often rely on subjective or noisy reward models, making stable policy optimization far more difficult. GRPO’s per-group advantage estimation is highly compatible with settings where reward computation is transparent and objective, as in math (Figure 10).

---

Efficient Learning from Diverse Solution Attempts

Mathematical reasoning often requires the model to try multiple solution paths before arriving at a correct answer or elegant derivation. GRPO’s core mechanism — group sampling — directly supports this, as multiple outputs (“grouped rollouts”) are generated for each problem instance.

By comparing each solution’s reward to the group mean, GRPO enables the model to reinforce approaches that outperform common errors or naive guesses in the group. This fosters systematic exploration of problem-solving strategies and mitigates overfitting to spurious patterns that might arise from individual samples.

In practical terms, this approach enables rapid discrimination between valuable reasoning sequences and ineffective or “shortcut” answers commonly found in early-stage LLM outputs.

---

Post Tuning Qwen3 Using GRPO

In this section, we will see how to post-train small language models (e.g., Qwen3) using GRPO to improve their mathematical reasoning capabilities.

For this implementation, we will use the AI-MO/NuminaMath-TIR dataset, which contains 70K problems from the NuminaMath-CoT dataset, focusing on those with numerical outputs, most of which are integers.

The original NuminaMath-CoT dataset (containing 860,000 pairs of competition math problems and solutions) is designed to enhance the mathematical reasoning capabilities of large language models (LLMs). It stands as the largest dataset ever released in the field of mathematics. The NuminaMath dataset includes problems ranging from high school level to advanced competition level, all meticulously annotated with accompanying chain-of-thought traces (Table 1).

We will start by installing the necessary libraries.

pip install trl==0.14.0 peft math_verify
pip install -U datasets

---

Loading and Visualizing the Dataset

After setting up the environment, we will begin by loading our dataset and visualizing a few examples.

from datasets import load_dataset

dataset_id = "AI-MO/NuminaMath-TIR"
train_dataset, test_dataset = load_dataset(dataset_id, split=['train[:1%]', 'test[:10%]'])

print("Train set: ", len(train_dataset))
print("Test set: ", len(test_dataset))
from IPython.display import Markdown, display

display(Markdown(r"**Problem Statement**: " + train_dataset[0]["problem"]))
display(Markdown(train_dataset[0]["solution"]))

Output:

On Line 1, we import the load_dataset function from the datasets library, which enables access to a specific dataset by its ID. On Line 3, we define the dataset identifier. Then on Line 4, we use load_dataset to fetch small subsets of the train (1%) and test (10%) splits from the NuminaMath-TIR collection.

On Lines 6 and 7, we print the sizes of each subset for confirmation. Finally, on Lines 8-11, we use IPython’s Markdown display to beautifully render the problem statement and its solution from the first training sample right in the notebook (Figure 11).

Next, we convert our train and test data problem statements into conversational-style prompts.

def make_conversation(example):
    return {
        "prompt": [
            {"role": "user", "content": example["problem"]},
        ],
    }

train_dataset = train_dataset.map(make_conversation)
test_dataset = test_dataset.map(make_conversation)
display(train_dataset[0]['prompt'])

On Lines 12-17, we define a helper function make_conversation that transforms each dataset example into a structured dictionary with a single "prompt" entry — this includes the math problem as user input, formatted for chat-style training.

On Lines 19 and 20, we apply this mapping function to the train and test datasets, thereby converting the raw problem data into conversational form. Finally, on Line 21, we display the prompt from the first transformed training example to verify the new format, which aligns with dialogue-based model training.

---

Loading and Preparing the Qwen3 Model

Now, we start loading our model and defining our LoRA config for parameter-efficient finetuning (rather than fully finetuning all model parameters, which is costly) of Qwen3.

import torch
from transformers import AutoModelForCausalLM, AutoProcessor

model_id = "Qwen/Qwen3-0.6B"

# Load model and tokenizer
model = AutoModelForCausalLM.from_pretrained(
    model_id,
    device_map="auto",
    torch_dtype=torch.bfloat16
)

processor = AutoProcessor.from_pretrained(model_id)

from peft import LoraConfig, get_peft_model

# Configure LoRA
peft_config = LoraConfig(
    r=8,
    lora_alpha=8,
    lora_dropout=0.1,
    target_modules=["q_proj", "v_proj"],
)

# Apply PEFT model adaptation
peft_model = get_peft_model(model, peft_config)

# Print trainable parameters
peft_model.print_trainable_parameters()

Output:

trainable params: 1,146,880 || all params: 597,196,800 || trainable%: 0.1920

On Lines 22 and 23, we import the necessary PyTorch and Hugging Face classes to load a causal language model and its associated processor. On Line 25, we specify the model ID for Qwen3-0.6B. Then, on Lines 28-32, we load the model using AutoModelForCausalLM.from_pretrained() with auto device placement and bfloat16 precision for memory efficiency. On Line 34, we load the corresponding processor, which handles tokenization and input formatting.

On Line 36, we bring in the PEFT utilities for LoRA-based fine-tuning. On Lines 39-44, we set up LoraConfig, tweaking parameters like rank r, scaling factor lora_alpha, dropout rate, and targeting attention projection layers. On Line 47, we adapt the original model using this LoRA configuration to inject low-rank updates into the model weights. Finally, on Line 50, we print the trainable parameters — giving us insight into which parts of the model will be updated during training.

Below, we implement an inference function to generate the solution given a prompt using the above model.

import time

def generate_solution(model, prompt):
  # Build the prompt from the dataset
  prompt = " ".join(entry['content'] for entry in prompt)

  # Tokenize and move to the same device as the model
  inputs = processor(prompt, return_tensors="pt").to(model.device)

  # Generate text without gradients
  start_time = time.time()
  with torch.no_grad():
      output_ids = model.generate(**inputs, max_new_tokens=512)
  end_time = time.time()

  # Decode and extract model response
  generated_text = processor.decode(output_ids[0], skip_special_tokens=True)

  # Get inference time
  inference_duration = end_time - start_time

  # Get number of generated tokens
  num_input_tokens = inputs['input_ids'].shape[1]
  num_generated_tokens = output_ids.shape[1] - num_input_tokens

  return generated_text, inference_duration, num_generated_tokens

On Line 51, we import the time module to help track inference duration. Then on Line 53, we define generate_solution, a function that takes in a model and a structured prompt, joining the chat entries into a single text string. On Lines 55-58, we tokenize this prompt using the processor and move the inputs to the same device as the model for seamless execution.

On Lines 61-64, we measure the time taken to generate a response using torch.no_grad(), which avoids computing gradients — achieving speed and simplicity. On Line 67, we decode the generated tokens into readable text, skipping any special tokens.

Finally, on Lines 73-76, we return the generated output, its inference time, and token count for easy evaluation of model performance.

---

Implementing Verifiable Reward Functions

Since we are training our model for mathematical reasoning, we can use verifiable rewards for GRPO. To verify whether or not a generated solution is correct with respect to the original solution, we will use the Hugging Face Math-Verify library.

Math-Verify is a robust mathematical expression evaluation system designed for assessing Large Language Model outputs in mathematical tasks. This evaluator achieves the highest accuracy and the most correct scores compared to existing evaluators on the MATH dataset.

The code below implements our reward function, which assigns a higher reward if the generated solution is correct.

from math_verify import LatexExtractionConfig, parse, verify
def accuracy_reward(completions, **kwargs):
    """Reward function that checks if the completion is the same as the ground truth."""
    solutions = kwargs['solution']
    completion_contents = [completion[0]["content"] for completion in completions]
    rewards = []
    for content, solution in zip(completion_contents, solutions):
        try:
          gold_parsed = parse(solution, extraction_mode="first_match", extraction_config=[LatexExtractionConfig()])
          answer_parsed = parse(content, extraction_mode="first_match", extraction_config=[LatexExtractionConfig()])
          if len(gold_parsed) != 0:
            rewards.append(float(verify(answer_parsed, gold_parsed)))
          else:
              rewards.append(1.0)
        except:
          rewards.append(0.0)
    return rewards

On Line 77, we import utilities from the math_verify library, which enable LaTeX-based parsing and verification of mathematical content. Then, on Line 78, we define the accuracy_reward function that compares model-generated completions against ground truth solutions.

On Lines 80 and 81, we extract those solutions and pull out the generated content from the completions list. On Line 83, we loop through each predicted-answer pair, parse both using LaTeX extraction (configured to grab the first valid match), and apply verify() to check correctness.

If no gold answer is extractable, we assign a default reward of 1.0; otherwise, verification determines the reward. Errors during parsing or verification result in a fallback reward of 0.0. Finally, on Line 93, the full list of reward scores is returned.

The above code provides a basic implementation of a verifiable reward function that can be used in GRPO. Now we will test our model (without any GRPO training yet) using the accuracy reward function on a test data example to see how it performs.

example = test_dataset[4]

## Testing Generation
generated_text, inference_duration, num_generated_tokens = generate_solution(model, example['prompt'])
display(Markdown(generated_text))
print(f"Inference Duration: {inference_duration} seconds")
print(f"Number of Generated Tokens: {num_generated_tokens}")

## Testing Reward Function
solutions = [example['solution']]
completions = [[{"content": generated_text}]]
print(f"Accuracy Reward: {accuracy_reward(completions, solution=solutions)}")

Output:

As can be seen, the Qwen3 model, without any GRPO training, yet fails to answer the questions correctly and rather falls into a loop of confusion (Figure 12). In the next section, we will see if GRPO training can improve the model’s reasoning capabilities on the same example.

---

GRPO Training

We have everything in place for our GRPO training: the model, dataset, and reward function. It’s time to configure and start our GRPO training. We will utilize the Hugging Face TRL GRPOTrainer and GRPOConfig for quick and clean implementation.

from trl import GRPOConfig, GRPOTrainer

# Configure training arguments using GRPOConfig
training_args = GRPOConfig(
    output_dir="Qwen3-0.6B-NuminaMath-GRPO",
    learning_rate=1e-5,
    remove_unused_columns=False, # to access the solution column in accuracy_reward
    gradient_accumulation_steps=16,
    num_train_epochs=1,
    bf16=True,

    # Parameters that control de data preprocessing
    max_completion_length = 256,
    num_generations=4,
    max_prompt_length=512,

    # Parameters related to reporting and saving
    logging_steps=10,
    save_strategy="steps",
    save_steps=10,
)

trainer = GRPOTrainer(
    model=model,
    reward_funcs=[accuracy_reward],
    args=training_args,
    train_dataset=train_dataset.remove_columns(['messages', 'problem'])
)

trainer.train()
trainer.save_model(training_args.output_dir)

On Line 106, we import GRPOConfig and GRPOTrainer from the trl library to set up and run GRPO-style reinforcement learning. Then, on Lines 109-126, we configure the training parameters via GRPOConfig, setting the output directory, learning rate, LoRA compatibility (remove_unused_columns=False), batch accumulation, epochs, and precision type (bf16).

We also define generation controls (e.g., maximum prompt/completion lengths, and the number of completions per sample). Logging and checkpointing settings ensure progress is tracked and saved every few steps.

On Lines 128-133, we instantiate GRPOTrainer using the LoRA-adapted model, our accuracy_reward function, the training arguments, and a filtered dataset (excluding non-essential columns). Finally, on Lines 135 and 136, we launch the training and save the fine-tuned model to the configured directory.

Once training is complete, let’s try out our trained model on the same test data example and see how it performs.

example = test_dataset[4]

## Testing Generation
generated_text, inference_duration, num_generated_tokens = generate_solution(model, example['prompt'])
display(Markdown(generated_text))
print(f"Inference Duration: {inference_duration} seconds")
print(f"Number of Generated Tokens: {num_generated_tokens}")

## Testing Reward Function
solutions = [example['solution']]
completions = [[{"content": generated_text}]]
print(f"Accuracy Reward: {accuracy_reward(completions, solution=solutions)}")

Output:

As we see, after GRPO training and with <1000 examples, the model can now correctly answer complex mathematical problems (Figure 13).

---

---

Summary

Group Relative Policy Optimization (GRPO) is a reinforcement learning technique designed to overcome key limitations of Proximal Policy Optimization (PPO). We begin by recognizing that PPO suffers from high memory overhead due to its reliance on value networks, instability in value function estimation, and sensitivity to hyperparameters. GRPO addresses these issues by eliminating the need for a separate value function, instead using group-relative advantage estimation across multiple sampled completions. This not only reduces computational cost but also improves training stability and scalability.

We implement GRPO by defining a core objective that combines clipped surrogate loss with KL divergence regularization. By sampling multiple responses per prompt, we compute relative rewards and normalize them within each group, allowing the model to reinforce better-than-average completions. This setup is particularly effective for mathematical reasoning tasks, where verifiable reward functions (e.g., correctness checks and adherence to format) can be programmatically defined. GRPO’s ability to learn from diverse solution attempts and reward structured reasoning makes it ideal for domains requiring precision and logical consistency.

In our post-tuning workflow with Qwen3, we prepare the model using LoRA adapters for efficient fine-tuning and implement custom reward functions to guide the learning process. GRPO training proceeds by generating multiple completions, scoring them via deterministic heuristics, and updating the model to favor high-reward outputs. This approach enables us to align Qwen3’s outputs with desired reasoning formats and correctness criteria, resulting in a model that excels at structured problem-solving with minimal supervision.

---

Citation Information

Mangla, P. “Post Training Qwen3 for Math Reasoning Using GRPO,” PyImageSearch, P. Chugh, S. Huot, A. Sharma, and P. Thakur, eds., 2025, https://pyimg.co/tav5k

@incollection{Mangla_2025_post-training-qwen3-for-math-reasoning-using-grpo,
  author = {Puneet Mangla},
  title = {{Post Training Qwen3 for Math Reasoning Using GRPO}},
  booktitle = {PyImageSearch},
  editor = {Puneet Chugh and Susan Huot and Aditya Sharma and Piyush Thakur},
  year = {2025},
  url = {https://pyimg.co/tav5k},
}

---

To download the source code to this post (and be notified when future tutorials are published here on PyImageSearch), simply enter your email address in the form below!