Boolean Search: Harnessing AND, OR, and NOT Gates with Inverted Indexes

In this tutorial, you will learn the fundamentals of Information Retrieval (IR). We will start with the importance and applications of IR and then discuss fundamental concepts like documents, queries, indexing, ranking, and types of IR models (Boolean, vector space, probabilistic, etc.). We will implement our first IR model based on Term Incidence-based Boolean Retrieval. Lastly, we will end the lesson by understanding various metrics (Precision, Recall, F1 Score, mean Average Precision (mAP), Normalized Discounted Cumulative Gain (NDCG), etc.) used to evaluate IR models.

Boolean-Search-Gates-Inverted-Indexes-featured

This lesson is the 1st of a 3-part series on Unlocking the Power of Search: Boolean, Semantic, and Probabilistic Search Models Explained.

Boolean Search: Harnessing AND, OR, and NOT Gates with Inverted Indexes (this tutorial)
Diving into Semantic Search: Unraveling Vector Space Models, Jaccard and Cosine Similarities, and TF-IDF
Exploring Probabilistic Search: Unveiling the Binary Independence Model and the Power of the BM25 Algorithm

To learn how Boolean Search works, just keep reading.

Harnessing the Power of Boolean Search with Inverted Indexes

Ever wondered how Google search always gives you the relevant information for your query?

Information retrieval (IR) is a field that focuses on obtaining relevant information from large data sets. It’s a crucial aspect of search engines, databases, and information management systems.

In other words, Information Retrieval (IR) (Figure 1) is finding material (e.g., documents) of an unstructured nature (e.g., text, images, or videos) that satisfies an information need from within large collections (e.g., stored on computers). Unlike data retrieval, where the structure of data is known, IR deals with unstructured or semi-structured data (e.g., text documents, web pages, or multimedia).

Figure 1: Overview of an Information Retrieval System (source: Engati). — **Figure 1:** Overview of an Information Retrieval System (source: Engati).

Before starting with the basics, let’s see some of the real world applications of Information Retrieval.

The Role and Impact of Information Retrieval in Today’s Digital Age

Information retrieval (IR) is a pivotal component of the modern information landscape. Its importance is underscored by its wide range of applications across various scenarios. Here’s a detailed look at the significance of IR with practical applications and scenarios:

Search Engines: The most ubiquitous application of IR is in search engines like Google, Bing, or DuckDuckGo (Figure 2). Whenever a user types a query, the IR system quickly sifts through billions of web pages to present the most relevant results.

Figure 2: Application of Information Retrieval in Search Engines (source: Medium). — **Figure 2:** Application of Information Retrieval in Search Engines (source: Medium).

Digital Libraries: IR systems are used to manage large collections of digital content, making it easier for users to find specific books, articles, or documents. For example, a researcher looking for academic papers on a particular topic can retrieve relevant documents from databases (e.g., JSTOR, PubMed, or arXiv).
E-Commerce: Online shopping platforms (e.g., Amazon) use IR to help customers find products they want to purchase. For example, a customer searching for a “waterproof smartwatch” will be presented with a list of products that match or closely relate to their query.
Social Media: IR is used to filter and recommend content on social media platforms (e.g., Facebook, Instagram, Twitter (X)) based on user preferences and behavior. For example, a user interested in vegan recipes will see more posts related to vegan cooking in their feed. Here, IR algorithms are combined with recommendation algorithms to provide the most relevant recommendations to the user.
Customer Support: IR helps in retrieving information from FAQs and support documents to assist customers with their inquiries. A user having trouble with a software feature can get instant help through a chatbot that retrieves relevant support articles.

Understanding the Core Components of an Information Retrieval System

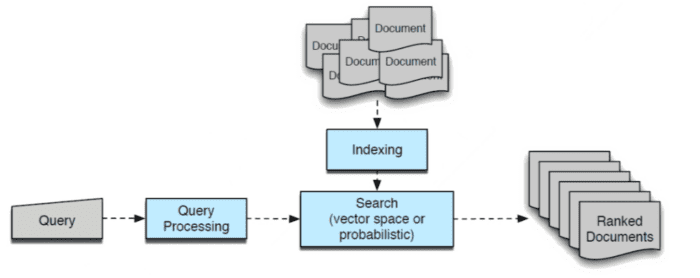
Let’s examine the core concepts and methodologies that form the foundation of IR. Figure 3 illustrates how various components of IR interact with each other. We will explain each of these components in detail below.

Figure 3: Various components of an IR system (source: BotPenguin). — **Figure 3:** Various components of an IR system (source: BotPenguin).

The Intricacies of Document Processing in Information Retrieval Systems

In IR, a document is any unit of content that can be retrieved and presented in response to a query. For example, a document can be a web page in the case of search engines, a text document in the case of digital libraries, an image in the case of Google images, a video in the case of YouTube or Netflix, or any other form of digital data that contains information.

Documents are the information repositories that the IR system aims to organize and search through. In a typical IR system, the number of documents can range from millions to billions, which makes the retrieval a challenging problem.

Optimizing Queries for Effective Information Retrieval

A query is a user’s request for information that can be expressed through a string of words (e.g., in search engines), audios (in the case of voice-enabled AI assistants like Alexa), phrases, or even a complex set of criteria. It represents what the user is seeking and can range from simple keyword searches to advanced queries using Boolean operators or other search syntax.

Query processing involves understanding and interpreting the user’s query to determine the intent and the information needed. Techniques (e.g., tokenization, stemming, and lemmatization) are used to break down and normalize the query. The IR system then uses the normalized queries to find and retrieve relevant documents.

The Science of Indexing: Organizing Data for Quick Retrieval

Indexing is the process of creating a mapping between a document and its location in a database. An efficient index allows the IR system to locate relevant documents quickly. In lay terms, Indexing is a way of organizing the unstructured data present in the form of documents.

Indexing involves creating machine-readable representations (e.g., vectors) for each document in the collection. These representations are typically selected words, terms, or phrases that encapsulate the main themes, subjects, and concepts of the content. They capture the content and features of the document, serve as entry points to access specific content, and provide a structured framework for organizing and searching information.

Advanced Selection and Ranking Algorithms in IR

Once the index is created, a selection or ranking algorithm decides which documents in the collection are relevant to the user query. These algorithms aim to sort a collection of documents or resources so that the most relevant ones appear first in response to a query.

Internally, these algorithms use various mathematical frameworks (e.g., cosine similarity, Jaccard similarity, and Boolean similarity) to measure a document’s relevance to the given query. In this series, we will discuss each strategy one by one.

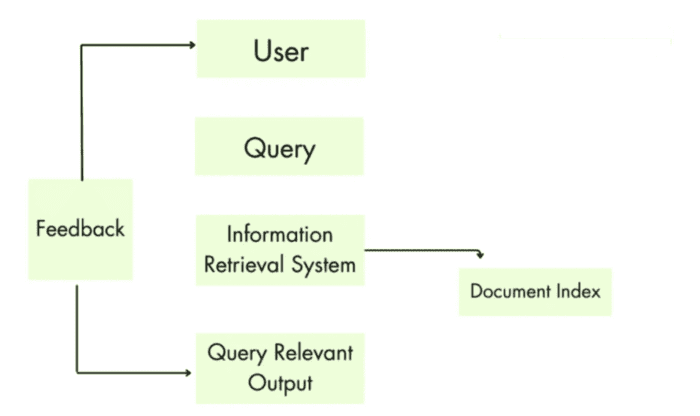
Enhancing Information Retrieval with Relevance Feedback

Relevance feedback in information retrieval is a process that involves the user in the retrieval process to improve the quality of the results. In a typical relevance feedback loop, a user first issues a short, simple query. The IR system then returns a set of documents that it thinks are relevant to the given user query.

The user reviews the results and marks some documents as relevant or non-relevant. Based on the user’s feedback, the IR system computes a new representation of the documents or possibly re-indexes the documents. The system then runs the refined query and returns a new set of results (based on the feedback).

The user can again provide new feedback by marking some documents (in new results) as relevant or non-relevant, and this process will be repeated.

Formulating Effective Information Retrieval Systems

The primary objective of an information retrieval system is to enable users to find relevant information from an organized collection of documents. Traditionally, IR systems dealt with textual documents, but modern systems can also handle multimedia information (e.g., text, audio, images, and video).

The formulation of IR often involves the use of set theory, Boolean algebra, and vector space models. Here’s a basic overview using mathematical notations:

Let $\mathcal{D}$ be the set of all documents in the collection and $q$ be a query represented as a set of terms or keywords. Each document $d \in \mathcal{D}$ has a representation $e(d)$ that captures the content and features of the document $d$ . The representation $e(d)$ can be a set of phrases, terms, or some vector or binary representation of the document.

Once we have the index representations $e(d)$ of all documents, the relevance of a document $d$ to a query $q$ is often represented by a relevance function:

$\text{rel}(e(d), q)$

which can be a binary value or a continuous score. Based on the relevance score $\text{rel}(e(d), q)$ , the IR algorithm can return top-K results (top-K documents having the highest relevance score with a query).

Understanding the Different Types of Information Retrieval Systems

Information Retrieval systems can be classified into the following types based on how the documents in a collection are represented, how queries are processed, or how query-document relevance is computed.

Boolean Retrieval Model Explained

In a Boolean retrieval model (Figure 4), documents and queries are represented using Boolean logic (AND, OR, NOT). It views documents and user queries as sets of terms, often referred to as a bag-of-words model. Document retrieval is based on the presence or absence of these terms in the documents and whether they satisfy the Boolean conditions specified in the query.

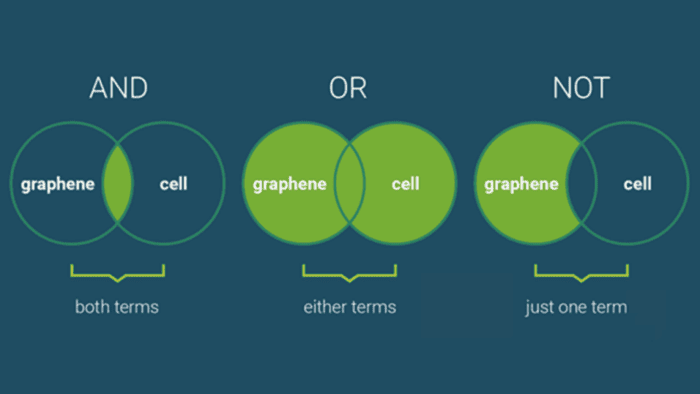
Figure 4: Boolean search models (source: Rodnik, "The Power of Boolean Search: Unleashing the Potential of Precise Information Retrieval," LinkedIn, 2023). — **Figure 4:** Boolean search models (source: Rodnik, “The Power of Boolean Search: Unleashing the Potential of Precise Information Retrieval,” *LinkedIn*, 2023).

In a Boolean retrieval model, a query is expressed as a Boolean expression using terms combined with Boolean operators:

AND: Retrieves documents that contain all the terms.
OR: Retrieves documents that contain any of the terms.
NOT: Excludes documents that contain the term.

For example, if a user inputs a query “apple AND juice”, the system will search for documents that contain both “apple” and “juice”.

Vector Space Model (VSM) for Information Retrieval

In this IR model, documents and queries are represented as fixed-dimensional vectors in a high-dimensional space (Figure 5). Each dimension in the vector representation corresponds to a term (word) in the collection. The similarity between a query vector and a document vector determines the relevance.

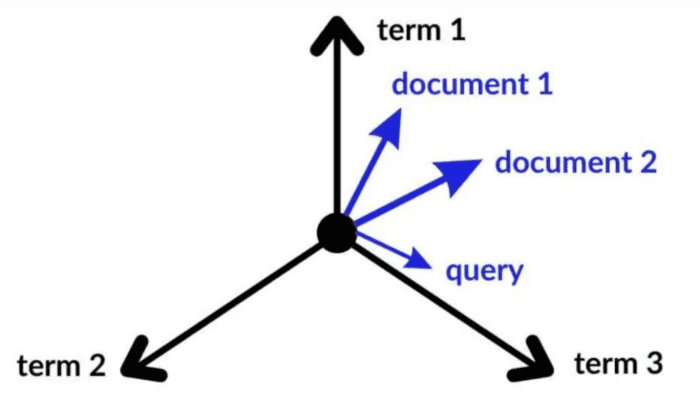
Figure 5: Vector space retrieval models (source: Van Otten, "Vector Space Model Made Simple With Examples & Tutorial In Python," Spot Intelligence, 2023). — **Figure 5:** Vector space retrieval models (source: Van Otten, “Vector Space Model Made Simple With Examples & Tutorial In Python,” *Spot Intelligence*, 2023).

These models can handle documents of arbitrary length, as each document is represented as a fixed-dimensional vector. For a practical example, consider a search engine. When you type a query, the search engine represents your query as a vector and computes its similarity with the vectors of all documents in its database. The documents with the highest similarity scores are then presented to you as search results.

Probabilistic Retrieval Models in IR Systems

Probabilistic retrieval models (Figure 6) are a class of information retrieval (IR) models that rank documents based on the probability that they are relevant to a given query. These models are grounded in the principles of probability theory and designed to reflect the uncertainty inherent in determining the relevance of documents to a user’s information needs.

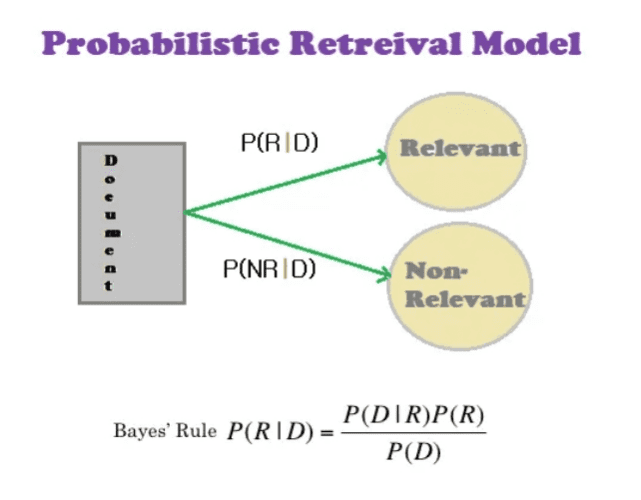
Figure 6: Probabilistic retrieval models (source: Analytics Vidhya). — **Figure 6:** Probabilistic retrieval models (source: Analytics Vidhya).

Probabilistic retrieval models are based on the probability-ranking principle which states that under certain assumptions, an IR system can achieve optimum retrieval performance by ranking documents in decreasing order of their probability of relevance to the user’s query.

Term-Document Incidence Matrix-Based Boolean Retrieval

The Boolean Retrieval model uses this matrix to process queries composed of Boolean expressions. The expressions can use the logical operators AND, OR, and NOT to combine terms. For example:

Term 1 AND Term 2 retrieves documents where both terms are present.
Term 1 OR Term 2 retrieves documents where at least one of the terms is present.
Term 1 AND NOT Term 2 retrieves documents where Term 1 is present and Term 2 is not.

The Term-Document Incidence Matrix is a foundational concept in the Boolean Retrieval model, one of the earliest and simplest models used in Information Retrieval (IR). It is a binary matrix that represents the presence (or absence) of terms in documents within a corpus. Before understanding the Term-Document Incidence Matrix in detail, let’s refresh the basics of Boolean algebra.

Boolean Algebra Basics and Its Application in IR

In Boolean algebra, we deal with binary values (1 and 0) representing true and false, respectively. The basic operations are:

AND (conjunction): A ∧ B is true if both A and B are true. Here, ∧ is the AND operator.
OR (disjunction): A ∨ B is true if either A or B is true. Here, ∨ is the OR operator.
NOT (negation): ¬A is true if A is false. Here, ¬ is the negation operation.

Constructing a Term-Document Incidence Matrix

A term-document incidence matrix (Table 1) $M$ is a $m \times n$ binary matrix that represents the occurrence of terms in documents. Here, $m$ is the vocabulary, and $n$ is the number of documents in the collection. For example, consider a set of documents and a vocabulary of terms:

Term	Document 1	Document 2	Document 3
term 1	1	0	1
term 2	0	1	1
term 3	1	0	1

Table 1: Term-document Incidence matrix.

Here, $M_{ij}=1$ indicates the presence of a term $i$ in a document $j$ , and 0 indicates the absence. This way, we have a 0-1 vector for each term $i$ in the vocabulary represented as:

$M_i = \left[M_{i0}, M_{i1}, M_{i2}, \dotsc, M_{in} \right]$

To process a query $q$ , we convert it into a Boolean expression and then apply it to the incidence matrix. For instance, if the query is “Find documents with term 1 AND NOT term 2”, we perform the following operations:

Take the 0-1 vector for term 1: [1, 0, 1]
Take the complement of the vector for term 2: [1, 0, 0] (since NOT term 2)
Perform a bitwise AND operation: [1 AND 1, 0 AND 0, 1 AND 0] = [1, 0, 0]

The result indicates that Document 1 is relevant to the query. Thus, we can retrieve all the documents relevant to the given Boolean query.

Challenges and Limitations of the Term-Document Incidence Matrix

Consider $n$ = 1 million documents, each with about 1000 words. Assume a word occupies 7 bytes, on average, which is around 6GB of data in each document, including spaces and punctuation.

Say there are $m$ = 500K distinct terms among these documents, which means that our term-document incidence matrix is of shape 500K × 1M having half a trillion 0s and 1s.

However, it has no more than one billion 1s (1M documents × 1000 words = 1B 1s). In most cases, the term-document matrix is extremely sparse and occupies quadratic space.

So, how can we efficiently organize the documents for Boolean search? What’s a better representation? The idea is to record only the 1 position, which is known as the Inverted Index Approach.

For each term $t$ , we must store a list of all documents that contain the term $t$ (Figure 7). We identify each document by a $\text{docID}$ , a document serial number. The figure explains how they can organize the data using an inverted index approach.

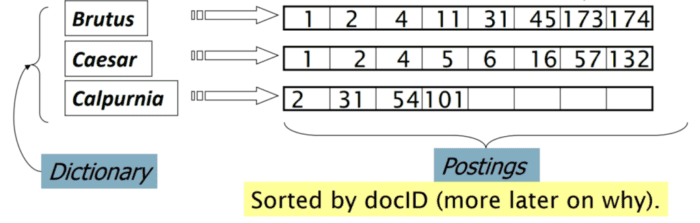
Figure 7: How the Inverted index works (source: Stanford). — **Figure 7:** How the Inverted index works (source: Stanford).

To implement the above data structure, we can store the document IDs for each term in linked lists or variable-length arrays.

Inverted Index Construction: The Foundation of Search Technologies

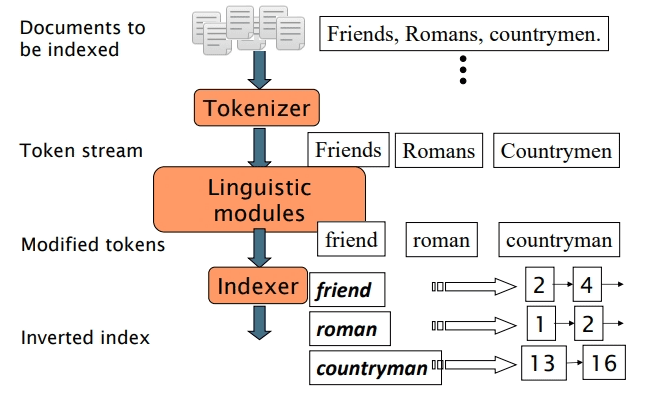
Text Preprocessing for Inverted Index Construction

Constructing an inverted index requires several steps (Figure 8). The first step is the text processing. Text processing pre-processes the terms in documents. It involves:

Tokenization: Cut character sequence into word tokens (e.g., “This is a cat” → [“This”, “is”, “cat”]).
Normalization: Map text and query term to the same form. For example, You want U.S.A. and USA to match.
Stemming: We may wish different forms of a root to match (e.g., authorize, and authorization should mean something similar).
Stopwords Removal: Remove common stopwords (e.g., “is”, “an”, “the”, etc.).

Figure 8: Construction of an Inverted Index (source: Stanford). — **Figure 8:** Construction of an Inverted Index (source: Stanford).

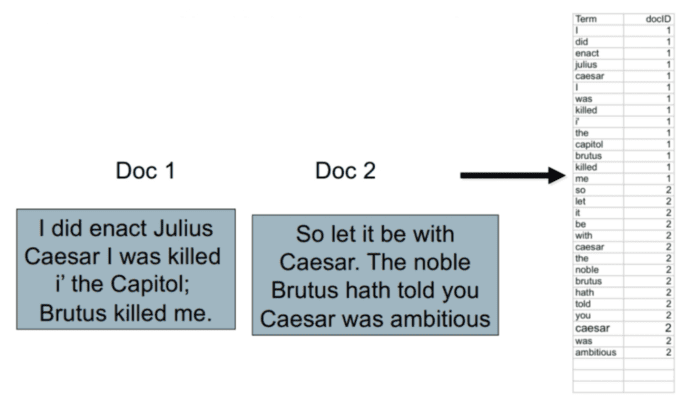
Creating Term-Document ID Pairs in Inverted Indexes

Generate a list of term-document ID pairs (Figure 9).

Figure 9: Generating a list of term-document ID pairs (source: Stanford). — **Figure 9:** Generating a list of term-document ID pairs (source: Stanford).

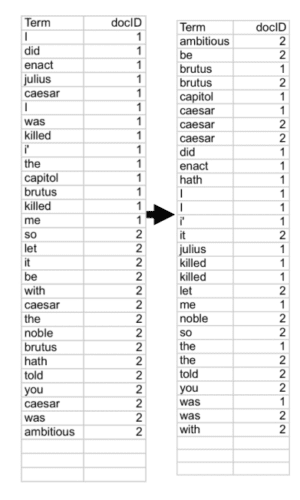
Sorting Term-Document IDs for Index Efficiency

Sort the term-document ID list by terms. If the term is the same, then sort by document ID (Figure 10).

Figure 10: Sorting the term-document ID list by terms (source: Stanford). — **Figure 10:** Sorting the term-document ID list by terms (source: Stanford).

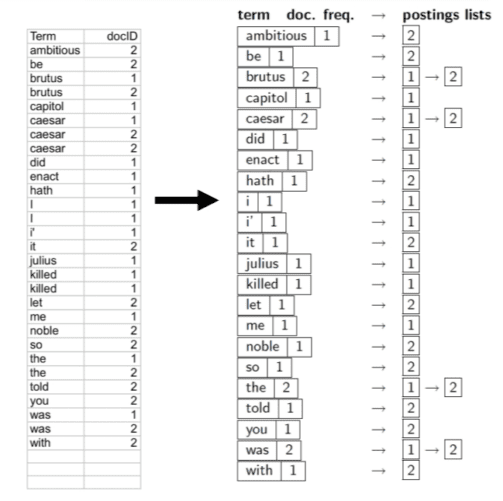
Optimizing Search with Dictionary and Postings in Inverted Indexes

Multiple term entries in a single document are merged and split into Dictionary and Postings (Figure 11). We can also add meta information (e.g., Documents) and frequency (the number of documents having that term) for each term. Such metadata can help in efficient query processing, as we will see later.

Figure 11: Creating a dictionary of postings, a.k.a. Inverted Index (source: Stanford). — **Figure 11:** Creating a dictionary of postings, a.k.a. Inverted Index (source: Stanford).

How to Build an Inverted Index for ArXiv Paper Abstracts

Now, let’s learn to implement a Boolean search model on the arXiv paper abstract dataset. The arXiv paper dataset consists of 50K+ paper titles and abstracts from various research areas.

The goal is to build a model that can retrieve relevant arXiv papers for a given Boolean query of form: term 1 AND term 2 OR term 3 AND term 4.

Step-by-Step Guide to Downloading the ArXiv Paper Abstract Dataset

We will download our arXiv paper abstract dataset using the Kaggle API. Here’s how you can install the Kaggle API and the arXiv dataset on your system:

$ pip install kaggle
$ kaggle datasets download -d spsayakpaul/arxiv-paper-abstracts
$ unzip <path-to-zip>/arxiv-paper-abstracts.zip -d /<path-to-data>/

Loading and Preparing the ArXiv Dataset for Analysis

Before loading our arXiv paper abstract dataset, let’s install some important Python libraries that we will use in this project:

nltk: The Natural Language Toolkit (NLTK) is a comprehensive Python library that provides a suite of tools for tasks such as tokenization, stemming, lemmatization, part-of-speech tagging, and named entity recognition.

contractions: This library is designed to standardize text data by expanding contractions in text, such as converting “don’t” to “do not” and “I’ll” to “I will.”

pandas: Pandas is a powerful and open-source Python library for data manipulation and analysis. We will use pandas to read and manipulate our datasets saved in CSV format.

numpy: NumPy is a popular Python library that supports large, multi-dimensional arrays and matrices, along with a large collection of high-level mathematical functions.

Here’s how to install the required Python libraries using pip.

$ pip install pandas numpy nltk contractions

Next, we will import these libraries into our Jupyter Notebook and load and visualize the dataset.

import numpy as np
import pandas as pd
import time
import re # for regular expressions
from collections import defaultdict
from nltk.stem import PorterStemmer
from nltk.corpus import stopwords
import contractions
import string
from IPython.display import display, HTML
import nltk

nltk.download('stopwords')

data = pd.read_csv("/content/arxiv_data.csv", header='infer')
print("Total rows : ", len(data))

display(HTML(data.head().to_html()))

On Lines 1-11, we import the pandas, numpy, time, collections, nltk, contractions, and string libraries. Next, on Line 13, we download the list of stopwords from the nltk package.

On Lines 15-18, we load the arxiv_data.csv using the pandas.read_csv() utility. We print the number of rows in the dataset and also visualize some of them using the IPython display. Here’s how the output of the above code block looks like (Figure 12):

Figure 12: Snapshot of an arXiv paper abstract dataset (source: Kaggle). — **Figure 12:** Snapshot of an arXiv paper abstract dataset (source: Kaggle).

Each row in the dataset has three fields:

titles: The title of the research paper.
summaries: The abstract of the research paper.
terms: Tags associated with the paper.

Text Preprocessing Techniques for Information Retrieval

Next, we implement a function preprocess() that takes a text (paper abstract in our case) as input and performs the following preprocessing operations:

# Preprocessing
def preprocess(text):
    stemmer = PorterStemmer()
    stop_words = set(stopwords.words("english"))

    # Text normalization
    expanded_words = []    
    for word in text.split():
      # using contractions.fix to expand the shortened words
      expanded_words.append(contractions.fix(word))  
   
    text = ' '.join(expanded_words)

    # Remove punctuations
    translator = str.maketrans("", "", string.punctuation)
    text = text.translate(translator)

    # Remove non-alphabetic characters
    text = re.sub(r"[^a-zA-Z\s]", "", text)  

    tokens = text.lower().split()

    # Stemming and stop-word removal
    tokens = [stemmer.stem(token) for token in tokens if token not in stop_words]
    return tokens

First, on Lines 21 and 22, we create an instance stemmer of PorterStemmer() for stemming and set stop_words consisting of all English stopwords.

Then, on Lines 25-30, we apply text normalization and canonicalization to the text by converting contracted words to their expanded form. For example, “it’s” to “it is”, “we’re” to “we are”, “goin'” to “going”, etc. For this, we use the Python contractions package.

On Lines 33-37, we remove punctuation marks like “?”, “!”, “.”, etc., as well as remove any non-alphabetical characters present in the text.

Finally, on Lines 39-42, we tokenize the text into tokens and apply stopword removal and stemming.

Constructing an Inverted Index from ArXiv Data

Here, we implement a construct_inverted_index() function that takes the data set and returns an inverted index that maps terms (or tokens) to the documents where they appear. We identify each document (an arXiv paper in our case) by an index, a document serial number.

# Inverted index construction
def construct_inverted_index(df):
  dictionary = {} # inverted index
 
  for index, row in df.iterrows():
    try:
      abstract_tokens = preprocess(row.summaries) # convert paper abstracts to tokens
      for token in abstract_tokens:
        if token not in dictionary: # add the document index to the postings of each term in the tokenized text
          dictionary[token] = [index]
        else:
          dictionary[token].append(index)
    except:
      continue
 
  #removing duplicates
  dictionary = {a:set(b) for a, b in dictionary.items()}
 
  return dictionary

inverted_index = construct_inverted_index(data)
print("Size of inverted index ", len(inverted_index))

On Line 46, we initialize an empty dictionary that will be our inverted index. Then, on Lines 48-50, we iterate through each document in the DataFrame and pre-process the abstract (e.g., tokenization, removing stopwords, etc.) of that document.

On Lines 51-55, for each token in the abstract:

If the token is not already in the dictionary, we add the document index to its postings list (a list of document indices).
Otherwise, we append the document index to the existing postings list for that token.

If any error occurs during processing (e.g., invalid abstract), it continues to the next document (Line 57).

On Line 60, after constructing the initial inverted index, we remove duplicate document indices from the postings lists (using sets instead of lists).

Finally, on Lines 64 and 65, we construct the inverted index by calling the construct_inverted_index() function on the arXiv paper abstract dataset.

Query Processing and Evaluation in Information Retrieval Systems

Let’s see how we can process queries and retrieve relevant documents using the inverted index approach.

Efficient Query Processing Techniques for Information Retrieval

Consider a Boolean query Brutus AND Caesar. To retrieve the relevant documents for this Boolean query, we will first retrieve the postings of both terms Brutus and Caesar (Figure 13).

Figure 13: Merging the postings of different terms in the Boolean query (source: Stanford). — **Figure 13:** Merging the postings of different terms in the Boolean query (source: Stanford).

Then, we will merge the postings of both terms to find the intersecting document IDs. To merge two postings (linked list of document IDs in our case), we will walk through the two postings simultaneously and check for the same document IDs. If the list lengths are $x$ and $y$ , the merge takes $O(x+y)$ operations.

The algorithm is shown in Figure 14.

Figure 14: Algorithm to compute the intersection of two postings (source: Stanford). — **Figure 14:** Algorithm to compute the intersection of two postings (source: Stanford).

Similarly, we can process other Boolean queries like:

A OR B: Take the union of postings of both terms A and B.
A AND (NOT B): Since we are looking for documents that do not contain term B, we need to negate the postings list for term B. This can be done by finding all documents that are not in the postings list for term B.

Then, we find the intersection of the postings list for term A and the negated postings list for term B. This gives us the documents that contain term A and do not contain term B.

Optimizing Information Retrieval Queries for Maximum Efficiency

Query optimization is the process of choosing the most efficient means of executing a given query by considering the possible query plans.

Generally, query optimization involves the following steps:

Parsing the Query: The first step in query optimization is parsing the query to understand its structure. This involves breaking down the query into its constituent parts (terms and operators) and building a query tree or similar structure.
Term Frequency: The frequency of each term in the document collection is considered. Terms that occur less frequently are more informative and are given higher priority.
Order of Evaluation: The order in which terms and operations are evaluated can significantly affect the speed of query processing. As a rule of thumb, NOT operations are performed first, followed by AND and then OR. Also, operations involving less frequent terms are performed first.
Use of Data Structures: Efficient data structures (e.g., skip pointers) in the posting lists can significantly speed up the process of finding intersections and unions.
Document-at-a-Time (DAAT) vs Term-at-a-Time (TAAT): In DAAT, each document is considered one at a time, and we check if it satisfies the query. In TAAT, we evaluate each term of the query against all documents before moving on to the next term. Depending on the query and the document collection, one approach may be faster than the other.

For example, consider a query that is an AND of $n$ terms:

$T_1 \ \text{ AND } \ T_2 \ \text{ AND } \ T_3, \dotsc, T_n$

To process this query (Figure 15), for each of the $n$ terms, get its postings, then AND them together.

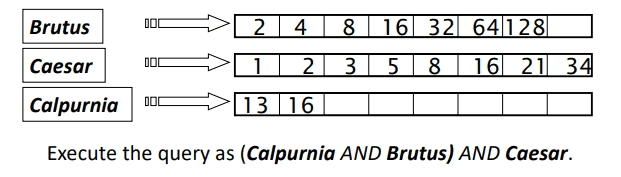
Figure 15: Query optimization for a Boolean query containing AND terms (source: Stanford). — **Figure 15:** Query optimization for a Boolean query containing `AND` terms (source: Stanford).

However, we can efficiently optimize the query using the following steps:

Sort the Terms by Document Frequency: The first step in optimizing the query is to sort the terms by their document frequency (i.e., the number of documents in which each term appears). This is based on the principle that less frequent terms are likely to eliminate more documents from consideration, thus reducing the computational cost of subsequent operations.
Use Short-Circuit Evaluation: Short-circuit evaluation is a programming concept where you stop evaluating an expression as soon as its outcome is determined. In the context of an AND query, if any term’s posting list is empty (i.e., the term appears in no documents), you can stop evaluation immediately because the AND of $n$ terms will be empty.
Use Document-at-a-Time (DAAT) Strategy: In the DAAT strategy, you consider one document at a time across all posting lists. If the document appears in all the posting lists, it satisfies the AND query. This strategy can be more efficient than the term-at-a-time (TAAT) strategy for AND queries because you can stop as soon as you find a document that is not in one of the posting lists.

Consider another example, (madding OR crowd) AND (ignoble OR strife). When you have a query that is a combination of AND and OR operations, you can optimize it using the following steps:

Parse the Query: The query is parsed into its constituent parts. In this case, we have two OR operations (madding OR crowd) and (ignoble OR strife), and an AND operation connecting them.
Evaluate OR Operations First: Since OR operations tend to increase the result set, it’s generally more efficient to evaluate them first. This way, when you perform the AND operation, you’re working with the largest possible sets, which makes the intersection operation more efficient.

This involves retrieving the postings lists for the terms madding, crowd, ignoble, and strife from the inverted index. The union of the postings lists for madding and crowd is taken, and the union of the postings lists for ignoble and strife is taken. These represent the sets of documents that match each of the OR operations.
Use Short-Circuit Evaluation: Short-circuit evaluation can also be used in this context. In the context of an AND query, if any term’s posting list is empty (i.e., the term appears in no documents), you can stop evaluation immediately because the AND of $n$ terms will be empty.

Implementing Query Processing in Information Retrieval Systems

Now that we have created the inverted index for our arXiv paper dataset, it’s time to see how we can process and evaluate the Boolean queries and retrieve relevant documents.

Converting Infix to Postfix Notation for Efficient Query Evaluation

The first process in query processing is to parse the given query and convert it to a format that is readable and easy to evaluate. Suppose we have a query: Given a query of form “term1 AND term2 OR NOT term3”.

The first step in query processing is to tokenize the given query into tokens. For the above example query, tokenization will result in the following list of tokens: [term1, "AND", term2, "OR", "NOT", term3]. In the code below, the tokenize_infix_expression() function implements the tokenization step.

Such an expression is known as an infix expression. Infix expressions are those expressions in which the operator is written in between the operands, such as “term1 AND term2”, “term2 OR NOT term3”, etc.

However, an infix expression is non-trivial to evaluate. To make the evaluation easier, we will convert this infix notation to a postfix notation or expression. Postfix expressions are those expressions in which the operator is written after the operands, such as:

Postfix for “term 1 AND term 2” is “term 1 term 2 AND”.
Postfix for “term 2 OR NOT term 3” is “term 2 term 3 NOT OR”.

Figure 16 illustrates how to convert an infix expression to a postfix expression using stack.

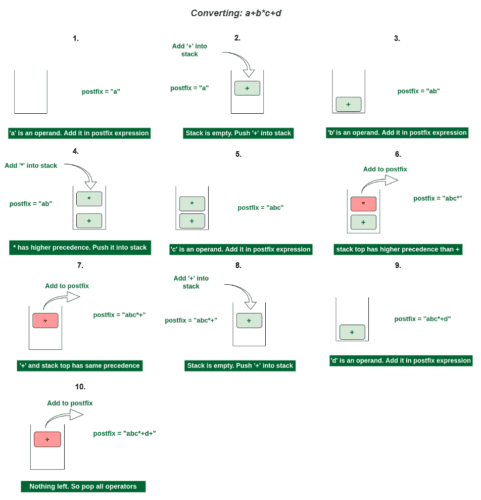
Figure 16: Converting an Infix expression to a Postfix expression (source: GeeksforGeeks). — **Figure 16:** Converting an Infix expression to a Postfix expression (source: GeeksforGeeks).

Here, the infix_to_postfix() function converts a Boolean infix expression to postfix notation.

# Infix to Postfix conversion
def tokenize_infix_expression(expression):
    return expression.split()

def infix_to_postfix(tokens):
    precedence = {"AND": 2, "NOT": 3, "OR":1 } # set the precedence of operators for postfix expression
    stack = []
    postfix = []

    for token in tokens:
        if token in precedence: # add operands first and then operators
            while stack and precedence.get(stack[-1], 0) >= precedence[token]:
                postfix.append(stack.pop())
            stack.append(token)
        elif token == '(':
            stack.append(token)
        elif token == ')':
            while stack and stack[-1] != '(':
                postfix.append(stack.pop())
            stack.pop()
        else:
            postfix.append(token)

    while stack:
        postfix.append(stack.pop())

    return postfix

On Line 67, the tokenize_infix_expression(expression) function takes an infix expression as a string and splits it into a list of tokens. This is done using the split() function, which splits the string at whitespace characters by default.

On Line 70, we implement the infix_to_postfix(tokens) function that takes a list of tokens (operands and operators) as input. On Line 71, a dictionary named precedence is defined to set the precedence of the operators. A higher value indicates higher precedence.

On Lines 72 and 73, we initialize two empty lists: stack and postfix. The stack temporarily holds operators and parentheses, while the postfix keeps the final postfix expression.

Then, on Line 75, we start the loop to iterate over each token in the input list.

On Lines 76-79, if the token is an operator, it pops operators from the stack to the postfix list as long as the operator on the top of the stack has equal or higher precedence. Then, it pushes the current operator onto the stack.
On Lines 80 and 81, if the token is an open parenthesis, it simply pushes it onto the stack.
On Lines 82-85, if the token is a close parenthesis, it pops operators from the stack to the postfix list until it finds an open parenthesis, which it pops and discards.
Finally, on Line 87, if the token is an operand, it simply appends it to the postfix list.

On Lines 89 and 90, after all tokens have been processed, the while loop pops any remaining operators from the stack to the postfix list.

Evaluating Postfix Notation: Efficient Query Execution

Now that we have the postfix expression for our Boolean query, we can evaluate it using stack. The idea is to keep adding operands to the stack until you encounter an operator in postfix notation. When we encounter an operator, we pop the required number of operands from stacks (2 for AND and OR operations and 1 for NOT operations), compute their result, and push back the result to the stack.

Figure 17 summarizes the algorithm to convert a postfix expression using stack.

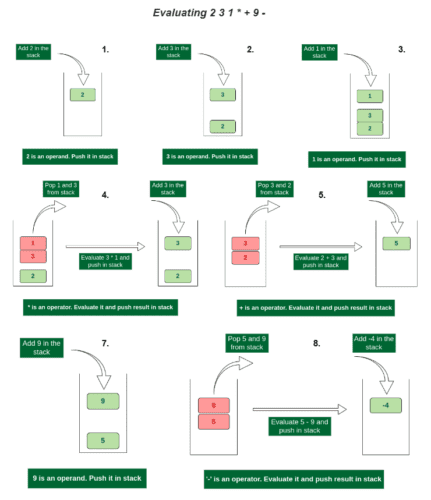
Figure 17: Evaluating a Postfix expression using stack (source: "Evaluation of Postfix Expression," GeeksforGeeks, 2023). — **Figure 17:** Evaluating a Postfix expression using stack (source: “Evaluation of Postfix Expression,” *GeeksforGeeks*, 2023).

The following code implements a evaluate_postfix() function that uses the stack and inverted index to process a Boolean query and return the indices of relevant documents.

# Evaluating postfix expression
def evaluate_postfix(postfix):
    stemmer = PorterStemmer()
    stack = []

    for token in postfix:
        if token == "AND": # take intersection of postings
            set2 = stack.pop()
            set1 = stack.pop()
            result = set1.intersection(set2)
            stack.append(result)
        elif token == "NOT": # finding all documents that are not in the postings list
            set1 = stack.pop()
            set2 = set(range(len(data)))
            result = set2.difference(set1)
            stack.append(result)
        elif token == "OR": # take union of postings
            set1 = stack.pop()
            set2 = stack.pop()
            stack.append(set1.union(set2))  # Convert token to a set
        else: # retrive the posting of the stemmed token
          stack.append(inverted_index.get(stemmer.stem(token), set()))
       

    return stack[0]

Firstly, on Line 95, a PorterStemmer object is created, which is used to stem the tokens in the postfix expression.

On Line 96, we initialize an empty list stack. This stack is used to store intermediate results during the evaluation of the postfix expression. Then, on Line 98, the function enters a loop over each token in the postfix expression:

If the token is an operator (“AND”, “NOT”, or “OR”), the function pops the necessary number of operands from the stack, performs the operation, and pushes the result back onto the stack.
Specifically, on Lines 99-103, the function pops two sets from the stack, computes their intersection (i.e., the set of documents that appear in both sets), and pushes the result back onto the stack.
On Lines 104-108, if the token is “NOT”, the function pops one set from the stack, computes the difference between the set of all documents and the popped set (i.e., the set of documents that do not appear in the popped set), and pushes the result back onto the stack.
On Lines 109-112, if the token is “OR”, the function pops two sets from the stack, computes their union (i.e., the set of documents that appear in either or both sets), and pushes the result back onto the stack.
Lastly, on Line 114, if the token is not an operator, it is assumed to be a term from the documents. The function stems the token using the stemmer object, retrieves the corresponding set of documents from the inverted index (or an empty set if the term does not appear in the index), and pushes this set onto the stack.

Testing and Validating Boolean Query Processing

Now that everything is in place, it’s time to test our Boolean model. The following code snippet tries a sample Boolean query to retrieve all the arXiv papers that are related to cancer detection (except lung cancer) and machine learning.

# Example query
infix_expression = "cancer AND detection AND machine AND learning AND NOT lung"

# Tokenize the expression
tokens = tokenize_infix_expression(infix_expression)

# Convert to postfix notation
postfix_expression = infix_to_postfix(tokens)
print(postfix_expression)
# # Evaluate the postfix expression
result = evaluate_postfix(postfix_expression)

titles = []
abstracts = []
for res in list(result)[:10]:
  titles.append(data.iloc[res].titles)
  abstracts.append(data.iloc[res].summaries.replace("\n", " "))

results = pd.DataFrame({"Title": titles, "Abstract": abstracts} )

display(HTML(results.to_html()))

On Lines 119-128, the infix expression cancer AND detection AND machine AND learning AND NOT lung is tokenized using the tokenize_infix_expression() function, converted to postfix notation using the infix_to_postfix() function, and then evaluated using the evaluate_postfix() function that we discussed earlier. The result of this evaluation is a set of document indices that match the search query.

Then, on Lines 130-138, the script retrieves the titles and abstracts of the first 10 documents in the result set and stores them in two lists. These lists are then used to create a pandas DataFrame, which is displayed as an HTML table using the display function from the IPython.display module.

Here’s how the output of the above query looks (Figure 18):

Figure 18: Output relevant documents for the Boolean query (source: image by the author). — **Figure 18:** Output relevant documents for the Boolean query (source: image by the author).

Understanding Evaluation Metrics for Information Retrieval Systems

Evaluating an IR model is as important as building it. In this section, we will discuss several metrics that are commonly used to evaluate their performance.

Recall in Information Retrieval: Ensuring Comprehensive Document Retrieval

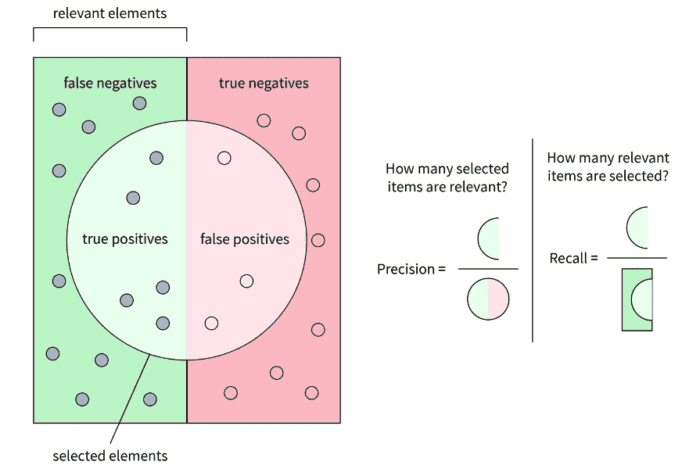
Recall assesses the IR system’s ability to retrieve all relevant documents from the database. It is calculated as the ratio of relevant documents retrieved to the total number of relevant documents available. The higher the recall, the higher the chances that the IR system will retrieve all relevant documents.

Let $R$ be the set of all relevant documents for a query $q$ in the collection and $\hat{R}$ be the set of documents retrieved by our IR system. Then, we can define Recall as:

$\text{Recall}(q) = \displaystyle\frac{\vert R \cap \hat{R} \vert }{\vert R \vert}$

For example, consider a query $q$ with relevant documents as $R = \{ d_1, d_3, d_5, d_7 \}$ . The IR system retrieves the following documents for the given query: $\hat{R} = \{ d_1, d_2, d_3, d_4, d_6, d_7\}$ . In this case, the Recall of the IR system for a given query is:

$\text{Recall}(q) = \displaystyle\frac{\vert R \cap \hat{R} \vert }{\vert R \vert} = \displaystyle\frac{3}{4} = 0.75$

This is illustrated in Figure 19.

Figure 19: Precision vs. Recall in Information Retrieval (source: Scaler). — **Figure 19:** Precision vs. Recall in Information Retrieval (source: Madala, “Introduction to Information Retrieval in NLP,” *Scaler*, 2023).

Precision: Accuracy in Information Retrieval

Precision measures the accuracy of the IR system in retrieving relevant documents. It is defined as the ratio of relevant documents retrieved to the total number of documents retrieved. The higher the precision, the higher the chances that the documents retrieved by the IR system are relevant to the given query.

Let $R$ be the set of relevant documents (in decreasing order of their relevance) for a query $q$ in the collection and $\hat{R}$ be the set of documents retrieved by our IR system. Then, we can define Precision as:

$\text{Precision}(q) = \displaystyle\frac{\vert R \cap \hat{R} \vert }{\vert \hat{R} \vert }$

$\text{Precision}(q) = \displaystyle\frac{\vert R \cap \hat{R} \vert }{\vert \hat{R} \vert } = \displaystyle\frac{3}{6} = 0.5$

This is also illustrated in Figure 19:

By default, precision $\text{Precision}(q)$ takes all the retrieved documents $R$ into account. However, it can also be evaluated at a given number of retrieved documents, commonly known as cut-off rank $k$ , where the model is assessed by considering only the first $k$ retrieved results (i.e., $\hat{R}[0], \hat{R}[1], \dotsc, \hat{R}[k-1]$ ). The measure is called precision at $k$ or $\text{Precision}(q)@k$ .

For example, in Figure 20, assume the IR system retrieves some $n$ documents $G^\prime = \{d_1, d_2, \dotsc, d_n \}$ out of which the 1st, 4th, and 5th documents are relevant. The $\text{Precision}(q)@k$ for different values of $k$ can be computed as follows:

$\text{Precision}(q)@1 = \displaystyle\frac{\vert \{ d_1 \} \vert }{\vert \{ d_1 \} \vert } = \displaystyle\frac{1}{1} = 1$

$\text{Precision}(q)@2 = \displaystyle\frac{\vert \{ d_1 \} \vert }{\vert \{ d_1, d_2 \} \vert} = \displaystyle\frac{1}{2} = 0.5$

$\text{Precision}(q)@3 = \displaystyle\frac{\vert \{ d_1 \} \vert }{\vert \{ d_1, d_2, d_3 \} \vert} = \displaystyle\frac{1}{3} = 0.22$

$\text{Precision}(q)@4 = \displaystyle\frac{\vert \{ d_1, d_4 \} \vert }{\vert \{ d_1, d_2, d_3, d_4 \} \vert} = \displaystyle\frac{2}{4} = 0.5$

$\text{Precision}(q)@5 = \displaystyle\frac{\vert \{ d_1, d_4, d_5 \} \vert }{\vert \{ d_1, d_2, d_3, d_4, d_5 \} \vert} = \displaystyle\frac{3}{4} = 0.6$

$\text{Precision}(q)@n = \displaystyle\frac{\vert \{ d_1, d_4, d_5 \} \vert }{\vert \{ d_1, d_2, \dotsc, d_n \} \vert} = \displaystyle\frac{3}{n} = 0.5$

Figure 20: Computing precision@K (source: Towards Data Science). — **Figure 20:** Computing precision@K (source: Tan, “Breaking Down Mean Average Precision (mAP),” *Towards Data Science*, 2019).

F1 Score: Balancing Precision and Recall

The F1 score is the harmonic mean of precision and recall, providing a balance between both precision and recall. A higher F1 score means that documents retrieved by the IR model are relevant and cover all the relevant documents. Mathematically, we can define the F1 score as:

$\text{F1}(q) = \displaystyle\frac{2 \times \text{Precision}(q) \times \text{Recall}(q)}{\text{Precision}(q) + \text{Recall}(q)}$

Average Precision (AP): Enhancing Information Retrieval with AP Scores

Average Precision (AP) (Figure 21) for a single query is the average of the precision scores after each relevant document is retrieved. Average precision is a good measure when a query can have multiple relevant documents. The formula for AP is:

$\text{AP}(q) = \displaystyle\frac{\sum\limits_{k=1}^n \text{Precision}@k \times \text{rel}(k) }{\vert R \vert}$

where $\text{Precision}@k$ is the precision at cut-off ( $k$ ) in the list, ( $\text{rel}(k)$ ) is an indicator function denoting the relevance of the $k\text{th}$ document (1 if relevant, 0 otherwise), and $\vert \hat{R} \vert$ is the number of retrieved documents.

Figure 21 illustrates how to compute the average precision.

Figure 21: Computing Average Precision (source: Towards Data Science). — **Figure 21:** Computing Average Precision (source: Tan, “Breaking Down Mean Average Precision (mAP),” *Towards Data Science*, 2019).

Mean Average Precision (mAP): Evaluating IR Systems Across Multiple Queries

mAP extends the Average Precision (AP) metric by calculating the average precision across different recall levels. It is particularly useful when queries can have multiple relevant documents.

For a set of queries, mAP is the mean of the Average Precision scores for each query. mAP is defined as:

$\text{mAP} = \displaystyle\frac{\sum\limits_{q=1}^Q \text{AP}(q)}{Q}$

where ( $Q$ ) is the number of queries.

Normalized Discounted Cumulative Gain (NDCG): Ranking Relevance in IR Systems

NDCG accounts for the position of the relevant documents in the result list, giving higher importance to hits at the top of the list. It is based on the premise that highly relevant documents appearing lower in a search result list should be penalized as the graded relevance value is reduced logarithmically proportional to the position of the result.

The Discounted Cumulative Gain (DCG) up to position $p$ is:

$\text{DCG}p = \sum\limits_{i=1}^p \displaystyle\frac{\text{rel}_i}{\log_2(i+1)}$

where $\text{rel}_i$ is the graded relevance of the result at position $i$ .

In graded relevance, each document is assigned a relevance label. In binary relevance, it’s either relevant (1) or not relevant (0). In multi-graded relevance, labels range from 0 (not relevant) to a maximum value (e.g., 4). The maximum value of multi-graded relevance depends on the problem set.

NDCG is then obtained by normalizing the DCG by the ideal DCG (IDCG), which is the DCG obtained by placing the relevant documents in the ideal order:

$\text{NDCG}p = \displaystyle\frac{\text{DCG}p}{\text{IDCG}p}$

What's next? We recommend PyImageSearch University.

Course information:
86 total classes • 115+ hours of on-demand code walkthrough videos • Last updated: October 2024
★★★★★ 4.84 (128 Ratings) • 16,000+ Students Enrolled

I strongly believe that if you had the right teacher you could master computer vision and deep learning.

Do you think learning computer vision and deep learning has to be time-consuming, overwhelming, and complicated? Or has to involve complex mathematics and equations? Or requires a degree in computer science?

That’s not the case.

All you need to master computer vision and deep learning is for someone to explain things to you in simple, intuitive terms. And that’s exactly what I do. My mission is to change education and how complex Artificial Intelligence topics are taught.

If you're serious about learning computer vision, your next stop should be PyImageSearch University, the most comprehensive computer vision, deep learning, and OpenCV course online today. Here you’ll learn how to successfully and confidently apply computer vision to your work, research, and projects. Join me in computer vision mastery.

Inside PyImageSearch University you'll find:

✓ 86 courses on essential computer vision, deep learning, and OpenCV topics
✓ 86 Certificates of Completion
✓ 115+ hours of on-demand video
✓ Brand new courses released regularly, ensuring you can keep up with state-of-the-art techniques
✓ Pre-configured Jupyter Notebooks in Google Colab
✓ Run all code examples in your web browser — works on Windows, macOS, and Linux (no dev environment configuration required!)
✓ Access to centralized code repos for all 540+ tutorials on PyImageSearch
✓ Easy one-click downloads for code, datasets, pre-trained models, etc.
✓ Access on mobile, laptop, desktop, etc.

Click here to join PyImageSearch University

Summary: Exploring Information Retrieval Systems and Boolean Search

In this blog post, we delve into the intricate world of Information Retrieval (IR) systems, with a special focus on the Boolean search models and their efficient implementation via inverted indexes. We started by highlighting the importance and applications of IR across diverse domains, and its critical role in sifting through and retrieving information from large data repositories.

Next, we outlined the fundamental components of an IR system, which include documents, queries, indexing, selection, and ranking algorithms. We explored the concept of relevance feedback, a feature that enhances search results based on user interactions.

As we discussed the formulation of Information Retrieval, we compared various retrieval models (e.g., the Boolean Model, Vector Space Model (VSM), and Probabilistic Retrieval Model). Each model offers a distinct method for processing queries and documents.

Subsequently, we explored Boolean Retrieval through the Term-Document Incidence Matrix. We explained the fundamentals of Boolean Algebra and the steps involved in constructing the Term-Document Incidence matrix. We acknowledged the limitations of this approach, especially when dealing with voluminous datasets.

To overcome these limitations, we turned to Inverted-Index Construction. We detailed the process from text preprocessing to creating a token sequence, sorting, and establishing the dictionary and postings. We also covered efficient query processing and optimization techniques.

Finally, we reviewed essential evaluation metrics such as Recall, Precision, F1 Score, Average Precision (AP), and Normalized Discounted Cumulative Gain (NDCG). These metrics are crucial for evaluating the relevance of search results and the overall efficacy of the IR system.

In summary, this blog post serves as an extensive primer on the mechanics of IR systems, particularly emphasizing Boolean search and inverted indexes, and offers valuable insights into both the theoretical framework and practical applications of information retrieval technologies.

Citation Information

Mangla, P. “Boolean Search: Harnessing AND, OR, and NOT Gates with Inverted Indexes,” PyImageSearch, P. Chugh, A. R. Gosthipaty, S. Huot, K. Kidriavsteva, and R. Raha, eds., 2024, https://pyimg.co/wk9r2

@incollection{Mangla_2024_IR_Boolean-Search-Inverted-Indexes,
  author = {Puneet Mangla},
  title = {Boolean Search: Harnessing AND, OR, and NOT Gates with Inverted Indexes},
  booktitle = {PyImageSearch},
  editor = {Puneet Chugh and Aritra Roy Gosthipaty and Susan Huot and Kseniia Kidriavsteva and Ritwik Raha},
  year = {2024},
  url = {https://pyimg.co/wk9r2},
}

Join the PyImageSearch Newsletter and Grab My FREE 17-page Resource Guide PDF

Enter your email address below to join the PyImageSearch Newsletter and download my FREE 17-page Resource Guide PDF on Computer Vision, OpenCV, and Deep Learning.

What's next? We recommend PyImageSearch University.

Join the PyImageSearch Newsletter and Grab My FREE 17-page Resource Guide PDF

About the Author

Exploring Oobabooga Text Generation Web UI: Installation, Features, and Fine-Tuning Llama Model with LoRA

No Module Named ‘torch’

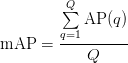
Comment section

Similar articles

You can learn Computer Vision, Deep Learning, and OpenCV.

Footer

Topics

Books & Courses

PyImageSearch

Access the code to this tutorial and all other 500+ tutorials on PyImageSearch

What's included in PyImageSearch University?