We can’t stop here, this is bat country.
Just a few days ago, the Google Research blog published a post demonstrating a unique, interesting, and perhaps even disturbing method to visualize what’s going inside the layers of a Convolutional Neural Network (CNN).
Note: Before you go, I suggest taking a look at the images generated using bat-country — most of them came out fantastic, especially the Jurassic Park images.
Their approach works by turning the CNN upside down, inputting an image, and gradually tweaking the image to what the network “thinks” a particular object or class looks like.
The results are breathtaking to say the least. Lower levels reveal edge-like regions in the images. Intermediate layers are able to represent basic shapes and components of objects (doorknob, eye, nose, etc.). And lastly, the final layers are able to form the complete interpretation (dog, cat, tree, etc.) — and often in a psychedelic, spaced out manner.
Along with their results, Google also published an excellent IPython Notebook allowing you to play around and create some trippy images of your own.
The IPython Notebook is indeed fantastic. It’s fun to play around with. And since it’s an IPython Notebook, it’s fairly easy to get started with. But I wanted to take it a step further. Make it modular. More customizable. More like a Python modules that acts and behaves like one. And of course, it has to be pip-installable (you’ll need to bring your own Caffe installation).
That’s why I put together bat-country, an easy to use, highly extendible, lightweight Python module for inceptionism and deep dreaming with Convolutional Neural Networks and Caffe.
Comparatively, my contributions here are honestly pretty minimal. All the real research has been done by Google — I’m simply taking the IPython Notebook, turning it into a Python module, while keeping in mind the importance of extensibility, such as custom step functions.
Before we dive into the rest of this post, I would like to take a second and call attention to Justin Johnson’s cnn-vis, a command line tool for generating inceptionism images. His tool is quite powerful and more like what Google is (probably) using for their own research publications. If you’re looking for a more advanced, complete package, definitely go take a look at cnn-vis. You also might be interested in Vision.ai’s co-founder Tomasz Malisiewicz’s clouddream docker image to quickly get Caffe up and running.
But in the meantime, if you’re interested in playing around with a simple, easy to use Python package, go grab the source from GitHub or install it via pip install bat-country
The rest of this blog post is organized as follows:
- A simple example. 3 lines of code to generate your own deep dream/inceptionism images.
- Requirements. Libraries and packages required to run
bat-country(mostly just Caffe and its associated dependencies). - What’s going on under the hood? The anatomy of
bat-countryand how to extend it. - Show and tell. If there is any section of this post that you don’t want to miss, it’s this one. I have put together a gallery of some really awesome images generated I generated over the weekend using
bat-country. The results are quite surreal, to say the least.
bat-country: an extendible, lightweight Python package for deep dreaming with Caffe and CNNs
Again, I want make it clear that the code for bat-country is heavily based on the work from the Google Research Team. My contributions here are mainly refactoring the code into a usable Python package, making the package easily extendible via custom preprocessing, deprocessing, step functions, etc., and ensuring that the package is pip-installable. With that said, let’s go ahead and get our first look at bat-country.
A simple example.
As I mentioned, one of the goals of bat-country is simplicity. Provided you have already installed Caffe and bat-country on your system, it only takes 3 lines of Python code to generate a deep dream/inceptionism image:
# we can't stop here...
bc = BatCountry("caffe/models/bvlc_googlenet")
image = bc.dream(np.float32(Image.open("/path/to/image.jpg")))
bc.cleanup()
After executing this code, you can then take the image returned by the dream method and write it to file:
result = Image.fromarray(np.uint8(image))
result.save("/path/to/output.jpg")
And that’s it! You can see the view source code of demo.py here on GitHub.
Requirements.
The bat-country packages requires Caffe, an open-source CNN implementation from Berkeley, to be already installed on your system. This section will detail the basic steps to get Caffe setup on your system. However, an excellent alternative is to use the Docker image provided by Tomasz of Vision.ai. Using the Docker image will get you up and running quite painlessly. But for those who would like their own install, keep reading.
Step 1: Install Caffe
Take a look at the official installation instructions to get Caffe up and running. Instead of installing Caffe on your own system, I recommend spinning up an Amazon EC2 g2.2xlarge instance (so you have access to the GPU) and working from there.
Step 2: Compile Python bindings for Caffe
Again, use the official install instructions from Caffe. Creating a separate virtual environment for all the packages from requirements.txt is a good idea, but certainly not required.
An important step to do here is update your $PYTHONPATH to include your Caffe installation directory:
export PYTHONPATH=/path/to/caffe/python:$PYTHONPATH
On Ubuntu, I also like to but this export in my .bashrc file so that it’s loaded each time I login or open up a new terminal, but that’s up to you.
Step 3: Optionally install cuDNN
Caffe works fine out of the box on the CPU. But if you really want to make Caffe scream, you should be using the GPU. Installing cuDNN isn’t too difficult of a process, but if you’ve never done it before, be prepared to spend some time working through this step.
Step 4: Set your $CAFFE_ROOT
The $CAFFE_ROOT directory is the base directory of your Caffe install:
export CAFEE_ROOT=/path/to/caffe
Here’s what my $CAFFE_ROOT looks like:
export CAFFE_ROOT=/home/ubuntu/libraries/caffe
Again, I would suggest putting this in your .bashrc file so it’s loaded each time you login.
Step 5: Download the pre-trained GoogLeNet model
You’ll need a pre-trained model to generate deep dream images. Let’s go ahead and use the GoogLeNet model which Google used in their blog post. The Caffe package provides a script that downloads the model for you:
$ cd $CAFFE_ROOT $ ./scripts/download_model_binary.py models/bvlc_googlenet/
Step 6: Install bat-country
The bat-country package is dead simple to install. The easiest way is to use pip:
$ pip install bat-country
But you can also pull down the source from GitHub if you want to do some hacking:
$ git clone https://github.com/jrosebr1/bat-country.git $ cd bat-country ... do some hacking ... $ python setup.py install
What’s going on under the hood — and how to extend bat-country
The vast majority of the bat-country code is from Google’s IPython Notebook. My contributions are pretty minimal, just re-factoring the code to make it act and behave like a Python module — and to facilitate easy modifications and customizability.
The first important method to consider is the BatCountry constructor which allows you to pass in custom CNNs like GoogLeNet, MIT Places, or other models from the Caffe Model Zoo. All you need to do is modify the base_path , deploy_path , model_path , and image mean . The mean itself will have to be computed from the original training set. Take a look at the BatCountry constructor for more details.
The internals of BatCountry take care of patching the model to compute gradients, along with loading the network itself.
Now, let’s say you wanted to override the standard gradient ascent function for maximizing the L2-norm activations for a given layer. All you would need to do is provide your custom function to the dream method. Here’s a trivial example of overriding the default behavior of the gradient ascent function to use a smaller step , and larger jitter :
def custom_step(net, step_size=1.25, end="inception_4c/output",
jitter=48, clip=True):
src = net.blobs["data"]
dst = net.blobs[end]
ox, oy = np.random.randint(-jitter, jitter + 1, 2)
src.data[0] = np.roll(np.roll(src.data[0], ox, -1), oy, -2)
net.forward(end=end)
dst.diff[:] = dst.data
net.backward(start=end)
g = src.diff[0]
src.data[:] += step_size / np.abs(g).mean() * g
src.data[0] = np.roll(np.roll(src.data[0], -ox, -1), -oy, -2)
if clip:
bias = net.transformer.mean["data"]
src.data[:] = np.clip(src.data, -bias, 255 - bias)
image = bc.dream(np.float32(Image.open("image.jpg")),
step_fn=custom_step)
Again, this is just a demonstration of implementing a custom step function and not meant to be anything too exciting.
You can also override the default preprocess and deprocess functions by passing in a custom preprocess_fn and deprocess_fn to dream :
def custom_preprocess(net, img):
# do something interesting here...
pass
def custom_deprocess(net, img):
# do something interesting here...
pass
image = bc.dream(np.float32(Image.open("image.jpg")),
preprocess_fn=custom_preocess, deprocess_fn=custom_deprocess)
Finally, bat-country also supports visualizing each octave, iteration, and layer of the network:
bc = BatCountry(args.base_model)
(image, visualizations) = bc.dream(np.float32(Image.open(args.image)),
end=args.layer, visualize=True)
bc.cleanup()
for (k, vis) in visualizations:
outputPath = "{}/{}.jpg".format(args.vis, k)
result = Image.fromarray(np.uint8(vis))
result.save(outputPath)
To see the full demo_vis.py script on GitHub, just click here.
Show and tell.
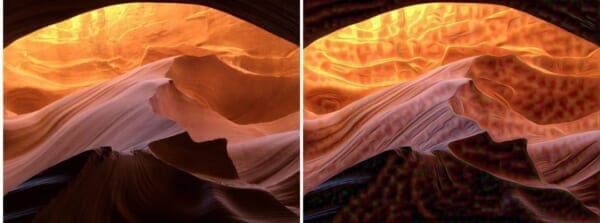
I had a lot of fun playing with bat-country over the weekend, specifically with images from Fear and Loathing in Las Vegas, The Matrix, and Jurassic Park. I also included a few of my favorite desktop wallpapers and photos from my recent vacation on the western part of the United States for fun.
For each of the original images (top), I have generated a “deep dream” using the conv2/3x3 , inception_3b/5x5_reduce , inception_4c/output layers, respectively.
The conv2/3x3 and inception_3b/5x5_reduce layers are lower level layers in the network that give more “edge-like” features. The inception_4c/output layer is the final output that generates trippy hallucinations of dogs, snails, birds, and fish.
Fear and Loathing in Las Vegas
Jurassic Park

The Matrix
Antelope Canyon (Page, AZ)
Angels Landing (Zion Canyon; Springdale, UT)
Zoo (Phoenix, AZ)
What's next? We recommend PyImageSearch University.
86+ total classes • 115+ hours hours of on-demand code walkthrough videos • Last updated: July 2025
★★★★★ 4.84 (128 Ratings) • 16,000+ Students Enrolled
I strongly believe that if you had the right teacher you could master computer vision and deep learning.
Do you think learning computer vision and deep learning has to be time-consuming, overwhelming, and complicated? Or has to involve complex mathematics and equations? Or requires a degree in computer science?
That’s not the case.
All you need to master computer vision and deep learning is for someone to explain things to you in simple, intuitive terms. And that’s exactly what I do. My mission is to change education and how complex Artificial Intelligence topics are taught.
If you're serious about learning computer vision, your next stop should be PyImageSearch University, the most comprehensive computer vision, deep learning, and OpenCV course online today. Here you’ll learn how to successfully and confidently apply computer vision to your work, research, and projects. Join me in computer vision mastery.
Inside PyImageSearch University you'll find:
- ✓ 86+ courses on essential computer vision, deep learning, and OpenCV topics
- ✓ 86 Certificates of Completion
- ✓ 115+ hours hours of on-demand video
- ✓ Brand new courses released regularly, ensuring you can keep up with state-of-the-art techniques
- ✓ Pre-configured Jupyter Notebooks in Google Colab
- ✓ Run all code examples in your web browser — works on Windows, macOS, and Linux (no dev environment configuration required!)
- ✓ Access to centralized code repos for all 540+ tutorials on PyImageSearch
- ✓ Easy one-click downloads for code, datasets, pre-trained models, etc.
- ✓ Access on mobile, laptop, desktop, etc.
Summary
In this blog post I introduced bat-country, an easy to use, highly extendible, lightweight Python module for inceptionism and deep dreaming with Convolutional Neural Networks and Caffe.
The vast majority of the code is based on the IPython Notebook published by the Google Research blog. My own contribution isn’t too exciting, I have simply (1) wrapped the code in a Python class, (2) made it easier to extend and customize, and (3) pushed it to PyPI to make it pip-installable.
If you are looking for a more robust deep dreaming tool using Caffe, I really suggest taking a look at Justin Johnson’s cnn-vis. And if you want to get your own Caffe installation up and running quickly (not to mention, one that has a web interface for deep dreaming), take a look a Tomasz’s docker instance.
Anyway, I hope you enjoy the bat-country ! Feel free to comment on this post with your own images generated using the package.

Join the PyImageSearch Newsletter and Grab My FREE 17-page Resource Guide PDF
Enter your email address below to join the PyImageSearch Newsletter and download my FREE 17-page Resource Guide PDF on Computer Vision, OpenCV, and Deep Learning.



















Thats great! seems the human face is computed after trying several faces like dogs,moneys etc!. I am going to learn deep learning 😀
Blow minded! It almost look like a painting from some surrealist pinter! Awesome! I’m eager to learn a little more about deep learning…
Thanks for this great post! Keep the good job.
Thanks Richard! 😀
Great work! I’m trying to get this running but keep running into the error:
Traceback (most recent call last):
File “./bat_country”, line 3, in
bc = batcountry(“caffe/models/bvlc_googlenet”)
TypeError: ‘module’ object is not callable
Any ideas? I’ve copied and pasted your example.
Hey Scott, the actual module is named
batcountry, but the class is namedBatCountry— notice how the ‘B’ and ‘C’ are capitalized. It looks like you may have manually typed the code out rather than copied and pasted. Change the line to:bc = BatCountry("caffe/models/bvlc_googlenet")and you won’t get an error.
Secondly, I would suggest cloning down the entire bat-country repo from GitHub and executing
demo.pydirectly.I get “NameError: name ‘BatCountry’ is not defined” when I execute the 3 lines
What do?
Hey Isaiah, you need to first install BatCountry using
pip install bat-country. That will install the package on your system. From there, I would suggest getting Caffe compiled and installed correctly as bat-country utilizes Caffe. Finally, take a look at the full demo.py file where those 3 lines came from. You’ll notice you’ll need to import the bat-country package:from batcountry import BatCountrybefore you can actually use it.Hi Adrian,
I had an idea for a project of using this to make random/interesting design recommendations on a model trained on thousands of construction drawings. Is Google DeepDream mainly showing eyes and dogs because it’s training data is overly skewed to eyes and dogs? Perhaps there’s more to it than that.
Hey Jeremy, you’re absolutely correct. Deep dream is showing more eyes/dogs because (1) there are many classes in ImageNet that contain eyes, and (2) dogs are heavily, heavily represented in the ImageNet dataset. If you wanted to show more construction related themes, you would need to train your own model using construction images. However, in the meantime, you may want to take a look at MIT Places model which does include more of a scene recognition and construction feel.
i broke free of the puppy slugs by changing the iterations by octave. google sets equal, for me, this introduces too much weight to the lower octaves, so i made mine run with curves, and no more puppy slug,. indeed the attractors seem to depend on the weight of the various octaves.
Is there an easy way to reference the layers rather than using their name? I’d like to call net.blob.key[5] or whatever, but can’t figure the syntax
Hey flow, you can access the layer names by using the
layersmethod:print bt.layers(). This will give you a list of strings corresponding to each layer in the network. Some can be used for deep dreaming, others can’t. But that should get you started.Hi Adrian,
Thanks for your great explanation. Could you detail how to use a different model? I downloaded alexnet via the script, but I when I run it and specify to use the model, I get this error from the bat-country module:
File “deep_dream.py”, line 5, in
bc = BatCountry(“caffe/models/bvlc_alexnet”)
File “/Library/Python/2.7/site-packages/batcountry/batcountry.py”, line 34, in __init__
channel_swap=channels)
File “/Users/michaelcaronna/caffe/python/caffe/classifier.py”, line 26, in __init__
caffe.Net.__init__(self, model_file, pretrained_file, caffe.TEST)
RuntimeError: Could not open file caffe/models/bvlc_alexnet/bvlc_googlenet.caffemodel
It seems to concatenate the alexnet model I specified with the googlenet model.
Thanks for the great resource,
Mike
Hey Mike — see the constructor to the BatCountry class. You’ll need to specify the
base_path, which you have done, but you’ll likely need to supply thedeploy_pathandmodel_path.You are right in saying that the code is concatenating the AlexNet model with the GoogLeNet model — hence you need to supply these paths explicitly.
Thanks so much!
No problem! 🙂
Hi Adrian,
Can I Install CAFFE on Raspberry?
Thanks for yaour sharing
It’s certainly possible, although I have never personally tried.
Hey Adrian,
I was wondering why is this take so long to create images. Essentially, all model runs in 4sec on my CPU, however, creating these images takes hours.
The larger your image is, the longer it will take to run. The same is true for your network.
Thanks Adrian. I make the images smaller and it is a lot faster now. However, I tried the smaller images with only model (without creating deep dream images), caffe almost run in the same time. That is interesting.
One more question,
I tried deep dreaming on the same image couple times and I realized I get slightly different image outputs. Do you have any idea why this is the case?
Deep learning networks are stochastic, meaning there a bit of randomness involved when training them. When running the deep dream code on your own images, the images must be passed through the network multiple times. The actual “dream” aspect of the code involves a bit of randomness, hence why your outputs are slightly different.