Table of Contents
- Approximate Nearest Neighbor with Locality Sensitive Hashing (LSH)
- What Is Locality Sensitive Hashing (LSH)?
- SimHash: LSH for Vector Databases
- Querying in LSH
- Hashing the Query Vector
- Accessing Relevant Buckets
- Retrieving Candidate Neighbors
- Computing Exact Distances
- Implementing SimHash for Similar Word Search
- Summary
Approximate Nearest Neighbor with Locality Sensitive Hashing (LSH)
In this tutorial, we will delve into the fundamental concepts and practical applications of Locality Sensitive Hashing (LSH) for finding approximate nearest neighbors in high-dimensional spaces. LSH is a powerful technique that allows us to perform similarity searches efficiently, making it an invaluable tool for dealing with large-scale datasets. Throughout this tutorial, we will explore how LSH works, understand its underlying principles, and learn how to implement it effectively for various use cases.
Consider a scenario where you have a massive collection of images, and you need to find images that are visually similar to a given query image. Traditional methods (e.g., brute-force search) become computationally expensive and impractical as the dataset grows. This is where LSH comes into play. By converting high-dimensional vectors into compact binary fingerprints, LSH enables quick and efficient comparison of images, significantly reducing the search time.
Another example is in the field of text document similarity. Imagine you have a vast library of documents and want to identify near-duplicate documents or find documents similar to a query document. LSH can efficiently handle this task by hashing the document vectors and grouping similar documents, allowing for rapid similarity searches.
By the end of this tutorial, you’ll have a solid understanding of how LSH works and how to implement it in your projects. Throughout this tutorial, we will explore how LSH works, understand its underlying principles, and learn how to implement it effectively for various use cases.
This lesson is the last in a 2-part series on Mastering Approximate Nearest Neighbor Search:
- Implementing Approximate Nearest Neighbor Search with KD-Trees
- Approximate Nearest Neighbor with Locality Sensitive Hashing (LSH) (this tutorial)
To learn how to implement LSH for approximate nearest neighbor search, just keep reading.
What Is Locality Sensitive Hashing (LSH)?
Locality Sensitive Hashing (LSH) is a technique used to perform approximate nearest neighbor searches in high-dimensional spaces. The core idea of LSH is to hash input items in such a way that similar items are more likely to be hashed into the same bucket. This approach significantly reduces the search space, making it feasible to find approximate nearest neighbors efficiently.
Figure 1 illustrates how an LSH table differs from a standard hash table. LSH tables are designed for similarity searches, grouping similar items using hash functions that preserve similarity. In contrast, standard hash tables are used for fast retrieval of exact key-value pairs, using hash functions that aim to distribute keys evenly.
Mathematical Foundation of LSH
LSH relies on a family of hash functions that are sensitive to the distance between items. Formally, a family of hash functions is called locality sensitive if it satisfies the following properties for a distance function
:
- For similar items: If
, then the probability that
and
hash to the same bucket is at least
.
- For dissimilar items: If
, then the probability that
and
hash to the same bucket is at most
.
Here, is a threshold distance,
is a constant, and
.
Figure 2 illustrates the locality sensitive hash functions.
Mathematically, this can be expressed as:
How LSH Works
- Hash Functions: Choose a family of hash functions
that is locality sensitive for the given distance metric. For example, for cosine similarity, random projection hash functions can be used.
- Hashing Data Points: Each point
in the dataset is hashed using multiple hash functions from
. This results in a set of hash values for each data point.
- Buckets: Data points are placed into buckets based on their hash values. Similar data points are likely to end up in the same bucket.
- Amplification: In order to improve search accuracy, multiple hash tables are used. Each table uses a different set of hash functions. This process is known as amplification and helps to ensure that similar items are more likely to collide in at least one of the hash tables.
- Query Processing: When a query point
is received, it is hashed using the same hash functions. The buckets corresponding to the hash values of
are retrieved from each hash table. The union of these buckets forms the candidate set.
- Refinement: The candidate set is then refined by computing the actual distances between the query point and the candidates to find the approximate nearest neighbors.
SimHash: LSH for Vector Databases
SimHash is a specific type of Locality Sensitive Hashing (LSH) designed to efficiently detect near-duplicate documents and perform similarity searches in large-scale vector databases. Developed by Moses Charikar, SimHash is particularly effective for high-dimensional data (e.g., text documents, images, and other multimedia content).
SimHash works by converting high-dimensional vectors into compact binary fingerprints, which can then be compared quickly. Given a vector in
-dimensional space, SimHash performs the following operations to compute the binary fingerprint of the vector.
Random Projection
The first step in the algorithm is to sample random vectors
in the same
-dimensional space as input vector
. Next, we project the input vector (Figure 3) with these random vectors to obtain a
-dimensional vector of dot products:
where is the dot product of
with random vector
.
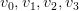 on random vector
on random vector 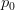 (source: softwaredoug).
(source: softwaredoug).Computing Binary Fingerprint
The -dimensional vector of dot products is then converted to an
-length binary representation as follows:
where the is the sign function (Figure 4) that returns
1 if the dot product is positive and 0 otherwise.
1 if the dot product is positive and 0 (or -1) if the dot product is negative (source: Randorithms).The binary vector (Figure 5) is known as the SimHash of the vector
.
 and
and 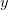 (source: Randorithms).
(source: Randorithms).A larger hash size generally increases precision because it reduces the likelihood of dissimilar items being hashed into the same bucket. However, it can also decrease recall because similar items might be split into different buckets.
A larger hash size reduces the probability of collisions between dissimilar items. This means that items that are not similar are less likely to end up in the same bucket, improving the accuracy of the search.
Mathematically, if we use a hash function that maps items to a binary string of length
, the probability of two dissimilar items
and
colliding (i.e.,
) decreases exponentially with
:
Creating Hash Table
After obtaining the SimHash , we create a hash table (Figure 6) with the key
. If the hash key is not present in the hash table, we create a new entry and add vector
. Otherwise, we add
to the existing list of vectors corresponding to key
.
A general trick to balance the trade-off between precision and recall is to use multiple hash tables. Each table uses a different set of hash functions. By increasing the hash size , each hash table becomes more precise, and the use of multiple tables ensures that recall remains high.
Mathematical Trade-Off
A larger hash size, , generally increases precision because it reduces the likelihood of dissimilar items being hashed into the same bucket. However, it can also decrease recall because similar items might be split into different buckets. Mathematically, we use a hash function
that maps items to a binary string of length
. In that case, the probability of two dissimilar items
and
colliding (i.e.,
) decreases exponentially with
:
By using multiple hash tables, each with a hash function of size , the probability that two similar items
and
are not hashed into the same bucket in any of the
tables is:
Querying in LSH
Now that we understand how SimHash works, let’s explore the querying process in LSH.
Hashing the Query Vector
Given a query vector , the same hash functions used to create the LSH tables are applied to hash
into binary fingerprints. This involves performing the random projection, computing the dot products, and converting them into the binary representation as described above.
where is the dot product of
with random vector
and
is the sign function.
Accessing Relevant Buckets
The binary fingerprint(s) of the query vector is used to access the corresponding buckets in the LSH tables. Since we might be using multiple hash tables, we access the buckets in each table where the query vector hashes.
For example, if we have hash tables, we look up the buckets:
where represents the binary fingerprint of the query vector in the
th hash table.
Retrieving Candidate Neighbors
The vectors stored in the accessed buckets are retrieved as potential candidates. These candidates are the vectors that are likely to be similar to the query vector due to the locality sensitive property of the hash functions.
Let be the set of candidate vectors retrieved from all accessed buckets:
Figure 7 shows how binary signatures can be used to find candidate pairs in LSH.
Computing Exact Distances
To find the true nearest neighbors among the candidates, we compute the actual distances (e.g., Euclidean distance) between the query vector and each candidate vector. This step ensures that the approximate nearest neighbors identified by the hash functions are accurately ranked.
For each candidate vector , compute the distance:
where is the
or Euclidean norm.
Implementing SimHash for Similar Word Search
In this section, we will see how LSH can help us fetch the nearest neighbors of a query in a quicker way using an approximate nearest neighbor search. We will implement a similar word search functionality that can fetch similar or relevant words to a given query word. For example, the relevant words to query the word
"computer" might look like "desktop", "laptop", "keyboard", "device", etc.
We will start by setting up libraries and data preparation.
Setup and Data Preparation
For implementing a similar word search, we will use the gensim library for loading pre-trained word embeddings vectors. If you don’t have gensim installed in your environment, you can do so via pip install gensim.
We load the pre-trained GloVe model (glove-twitter-25) using Gensim’s API, which provides 25-dimensional word vectors for more than 1 million words. These word vectors are trained from Twitter data making them semantically rich in information.
import gensim.downloader as api
import numpy as np
# Load the pre-trained Word2Vec model
model = api.load("glove-twitter-25")
# Extract all word embeddings into a dictionary
word_embeddings = {word: np.array(model[word]) for word in model.index_to_key}
print(len(word_embeddings.keys()), word_embeddings["computer"].shape)
On Lines 1 and 2, we import the necessary libraries:
gensim: for loading pre-trained word embeddingsnumpy: for numerical operations
On Line 5, we load the pre-trained GloVe model (glove-twitter-25) using the Gensim API. This model provides us with vector representations of words. On Line 8, we extract all word embeddings from the model into a dictionary called word_embeddings. Each word is mapped to its corresponding vector representation. Finally, on Line 9, we print the number of words in the dictionary and the shape of the embedding for the word "computer".
Setting Up Baseline with the k-NN Algorithm
With our word embeddings ready, let’s implement a -Nearest Neighbors (k-NN) search.
-NN search identifies the
closest points in a dataset to a given query point by calculating distances (usually Euclidean). It is useful in classification and regression tasks, finding patterns based on proximity.
However, the -Nearest Neighbors (k-NN) search algorithm is a brute-force algorithm that finds the nearest points by computing and comparing the distances of a query with all the instances in the corpus. This makes it impractical to use in large-scale applications where the size of search space can be billions (e.g., Google search, YouTube search, etc.).
Let’s see it ourselves by implementing and trying it out for our similar word application.
import time
def knn_search(word_embeddings, query_word, k=5):
# Ensure the query word is in the embeddings dictionary
if query_word not in word_embeddings:
raise ValueError(f"Word '{query_word}' not found in the embeddings dictionary.")
# Get the embedding for the query word
query_embedding = word_embeddings[query_word]
# Calculate the Euclidean distance between the query word and all other words
distances = {}
for word, embedding in word_embeddings.items():
if word != query_word: # Skip the query word itself
distance = np.linalg.norm(query_embedding - embedding)
distances[word] = distance
# Sort the distances and get the top k nearest neighbors
nearest_neighbors = sorted(distances, key=distances.get)[:k]
return nearest_neighbors
t1 = time.time()
nearest_neighbors = knn_search(word_embeddings, 'laptop', k=5)
t2 = time.time()
print(f"k-NN search took {t2-t1} seconds")
print("Retrieved neighbors : ", nearest_neighbors)
Output:
k-NN search took 8.236822128295898 seconds Retrieved neighbors : ['charger', 'wifi', 'tab', 'camera', 'ipod']
On Line 10, we import the time module to measure the execution time of the k-NN search.
On Lines 12-30, we define the knn_search function. On Lines 14 and 15, we check if the query word exists in the embeddings dictionary. On Line 18, we retrieve the embedding for the query word. On Lines 21-25, we calculate the Euclidean distance between the query word and all other words, storing these distances in a dictionary. On Line 28, we sort the distances and select the top k nearest neighbors.
Finally, on Lines 32-37, we measure the time taken to perform the -NN search and print the results. From the output, you can see that it took
-NN search slightly more than 9 seconds to retrieve the 5 similar words to the word
"laptop". This gives us an idea of the performance of our -NN implementation and sets a baseline for the LSH algorithm we will implement now.
Implementing SimHash
Now, we will demonstrate how we can implement the SimHash algorithm for optimized nearest neighbor searches in a set of word embeddings.
import numpy as np
from collections import defaultdict, Counter
class SimHash:
def __init__(self, hash_size, input_dim):
self.hash_size = hash_size
self.random_projection = np.random.normal(loc=0, scale=2.0, size=(hash_size, input_dim))
def _hash(self, vector):
projected_vector = np.dot(self.random_projection, vector)
hash_bits = np.zeros(self.hash_size)
for i in range(self.hash_size):
if projected_vector[i] > 1:
hash_bits[i] += 1
else:
hash_bits[i] -= 1
return ''.join(['1' if bit > 0 else '0' for bit in hash_bits])
def compute(self, vector):
return self._hash(vector)
class LSH:
def __init__(self, hash_size, input_dim, num_tables):
self.hash_size = hash_size
self.input_dim = input_dim
self.num_tables = num_tables
self.tables = [defaultdict(list) for _ in range(num_tables)]
self.hash_functions = [SimHash(hash_size, input_dim) for _ in range(num_tables)]
def _hash(self, vector, table_idx):
return self.hash_functions[table_idx].compute(vector)
def add(self, vector, word):
for i in range(self.num_tables):
hash_value = self._hash(vector, i)
self.tables[i][hash_value].append(word)
def query(self, vector):
candidates = set()
for i in range(self.num_tables):
hash_value = self._hash(vector, i)
candidates.update(self.tables[i][hash_value])
return candidates
lsh = LSH(hash_size=25, input_dim=25, num_tables=15)
for k, v in word_embeddings.items():
lsh.add(v, k)
In this code, we implement the SimHash and LSH (Locality Sensitive Hashing) algorithms to find approximate nearest neighbors efficiently. On Lines 38 and 39, we import the necessary libraries (i.e., numpy for numerical computations and defaultdict from the collections module) for creating default dictionaries.
On Lines 41-57, we define the SimHash class, which initializes with a hash size and input dimension. This class generates random projection vectors used for hashing input vectors. The _hash method computes the dot product of the input vector with the random projection vectors, converting the resulting projected vector into a binary hash based on the sign of the values. The compute method wraps the _hash method for easier access.
On Lines 59-80, we define the LSH class, which initializes with the hash size, input dimension, and number of hash tables. This class creates multiple hash tables and corresponding SimHash functions. The _hash method computes the SimHash for a given vector using the specified hash table.
The add method adds a vector and its corresponding word to the hash tables. In contrast, the query method retrieves candidate neighbors by accessing the relevant buckets in each hash table and collecting potential matches.
Finally, on Lines 82-84, we create an LSH instance and add word embeddings to the hash tables for similarity searches.
Next, we time the search for the nearest neighbors to the word "laptop", print the execution time, and retrieve the neighbors. After fetching the candidate neighbors of the query word, we compute the actual distances (e.g., Euclidean distance) between the query vector and each candidate vector to find the closest neighbors.
t1 = time.time()
query = "laptop"
k=5
candidates = lsh.query(word_embeddings[query])
distances = []
for word in candidates:
if word != query:
distances.append((word, np.linalg.norm(word_embeddings[query] - word_embeddings[word])))
result = sorted(distances, key=lambda x: x[1])[:k]
t2 = time.time()
print(f"SimHash query lookup took {t2-t1} seconds")
print(f"Candidates for the query vector: {result}")
Output:
SimHash query lookup took 0.006713390350341797 seconds
Candidates for the query vector: [('charger', 2.1116524), ('battery', 2.7517536), ('modem', 2.8823211), ('mic', 3.4616194), ('txt', 4.698156)]
From the output, we can see that SimHash is able to retrieve similar nearest neighbors as -NN search in milliseconds. This demonstrates the efficiency of the LSH in finding nearest neighbors compared to more straightforward, brute-force methods (e.g.,
-NN search).
Summary
In this comprehensive blog post, we delve into the concept of Locality Sensitive Hashing (LSH) and its application in efficiently finding approximate nearest neighbors in high-dimensional spaces. We start by introducing LSH and its mathematical foundation, which enables us to perform similarity searches quickly by converting high-dimensional vectors into binary fingerprints. The post provides a detailed explanation of how LSH works, including an example using cosine similarity with random projection to illustrate the process.
We then focus on SimHash, a specific type of LSH designed for vector databases. We break down the steps involved in SimHash, starting with random projection, computing the binary fingerprint, and creating hash tables. We discuss the mathematical trade-offs between precision and recall, and how using multiple hash tables can help balance these factors.
The querying process in LSH is thoroughly explained, covering the steps of hashing the query vector, accessing relevant buckets, retrieving candidate neighbors, and computing exact distances to identify the nearest neighbors.
Finally, we demonstrate how to implement SimHash for similar word searches. We guide you through the setup and data preparation, setting up a baseline with the -NN algorithm and implementing SimHash to achieve an efficient and scalable similarity search. By the end of this blog post, you’ll have a solid understanding of LSH and its practical applications, as well as the knowledge to implement it in your own projects for various use cases.
Citation Information
Puneet Mangla. “Approximate Nearest Neighbor with Locality Sensitive Hashing (LSH),” PyImageSearch, P. Chugh, S. Huot, and P. Thakur, eds., 2025, https://pyimg.co/5md9v
@incollection{Mangla_2025_approximate-nearest-neighbor-locality-sensitive-hashing-lsh,
author = {Puneet Mangla},
title = {{Approximate Nearest Neighbor with Locality Sensitive Hashing (LSH)}},
booktitle = {PyImageSearch},
editor = {Puneet Chugh and Susan Huot and Piyush Thakur},
year = {2025},
url = {https://pyimg.co/5md9v},
}
To download the source code to this post (and be notified when future tutorials are published here on PyImageSearch), simply enter your email address in the form below!

Download the Source Code and FREE 17-page Resource Guide
Enter your email address below to get a .zip of the code and a FREE 17-page Resource Guide on Computer Vision, OpenCV, and Deep Learning. Inside you'll find my hand-picked tutorials, books, courses, and libraries to help you master CV and DL!



Comment section
Hey, Adrian Rosebrock here, author and creator of PyImageSearch. While I love hearing from readers, a couple years ago I made the tough decision to no longer offer 1:1 help over blog post comments.
At the time I was receiving 200+ emails per day and another 100+ blog post comments. I simply did not have the time to moderate and respond to them all, and the sheer volume of requests was taking a toll on me.
Instead, my goal is to do the most good for the computer vision, deep learning, and OpenCV community at large by focusing my time on authoring high-quality blog posts, tutorials, and books/courses.
If you need help learning computer vision and deep learning, I suggest you refer to my full catalog of books and courses — they have helped tens of thousands of developers, students, and researchers just like yourself learn Computer Vision, Deep Learning, and OpenCV.
Click here to browse my full catalog.