Introduction to hyperparameter tuning with scikit-learn and Python

In this tutorial, you will learn how to tune machine learning model hyperparameters with scikit-learn and Python.

This tutorial is part one in a four-part series on hyperparameter tuning:

1. Introduction to hyperparameter tuning with scikit-learn and Python (today’s post)
2. Grid search hyperparameter tuning with scikit-learn ( GridSearchCV ) (next week’s post)
3. Hyperparameter tuning for Deep Learning with scikit-learn, Keras, and TensorFlow (tutorial two weeks from now)
4. Easy Hyperparameter Tuning with Keras Tuner and TensorFlow (final post in the series)

Tuning your hyperparameters is absolutely critical in obtaining a high-accuracy model. Many machine learning models have various knobs, dials, and parameters that you can set.

The difference between a very low-accuracy model versus a high-accuracy one is sometimes as simple as tuning the right dial. This tutorial will show you how to tune the dials on your machine learning model to boost your accuracy.

Specifically, we’ll be covering the basing of hyperparameter tuning by:

1. Obtaining a baseline with no hyperparameter tuning where we have a benchmark to improve
2. Exhaustively grid searching over a set of hyperparameters
3. Utilizing a random search to sample from a hyperparameter space

We’ll implement each method using Python and scikit-learn, train our model, and evaluate the results.

By the end of this tutorial, you’ll have a strong understanding of how to practically use hyperparameter tuning in your own projects to boost model accuracy.

To learn how to tune hyperparameters with scikit-learn and Python, just keep reading.

Introduction to hyperparameter tuning with scikit-learn and Python

In this tutorial, you will learn how to tune model hyperparameters using scikit-learn and Python.

We’ll start the tutorial by discussing what hyperparameter tuning is and why it’s so important.

From there, we’ll configure your development environment and review the project directory structure.

We’ll then have three Python scripts to implement:

1. One that trains a model with no hyperparameter tuning (so we can obtain a baseline)
2. One that utilizes an algorithm called “grid search” to exhaustively examine all combinations of hyperparameters — this method is guaranteed to do a full sweep of hyperparameter values, but also very slow
3. And a final method that uses a “random search” by sampling various hyperparameters from a distribution (not guaranteed to cover all hyperparameter values but in practice is typically just as accurate as grid search and runs far faster)

Finally, we’ll wrap up our tutorial with a discussion of the results.

What is hyperparameter tuning, and why is it important?

Have you ever tried using an old-school AM/FM radio before? You know, the analog radios that have knobs and dials you can move to select a station, adjust the equalizer, etc., like in Figure 1?

These radios may be a relic of the past, but if you’ve ever used one before, you know how important it is to get that station selector “just right.” If you let the station selector sit between two frequencies, you’ll get audio from two different stations bleeding into each other. The noise is cacophonous, and it’s near impossible to understand.

Similarly, machine learning models have all sorts of knobs and dials you can tune:

• Neural Networks have learning rate and regularization strength
• Convolutional Neural Networks have several layers, number of filters per convolutional layer, number of nodes in the fully connected layers, etc.
• Decision trees have the node split criteria (Gini index, information gain, etc.)
• Random Forests have the total number of trees in the forest, along with feature space sampling percentages
• Support Vector Machines (SVMs) have the type of kernel (linear, polynomial, radial basis function (RBF), etc.) along with any parameters you need to tune for the particular kernel

SVMs are notorious for requiring significant hyperparameter tuning, especially if you are using a non-linear kernel. Not only do you need to select the correct type of kernel for your data, but then you also need to tune any knobs and dials associated with the kernel — one wrong choice, and your accuracy can plummet.

Scikit-learn: hyperparameter tuning with grid search and random search

The two hyperparameter methods you’ll use most frequently with scikit-learn are a grid search and a random search. The general idea behind both of these algorithms is that you:

1. Define a set of hyperparameters you want to tune
2. Give these hyperparameters to the grid search or random search
3. These algorithms then automatically examine the hyperparameter search space and attempt to find the optimal values that maximize accuracy

That said, grid search and random search are inherently different techniques to hyperparameter tuning. Figure 2 visualizes these two hyperparameter search algorithms:

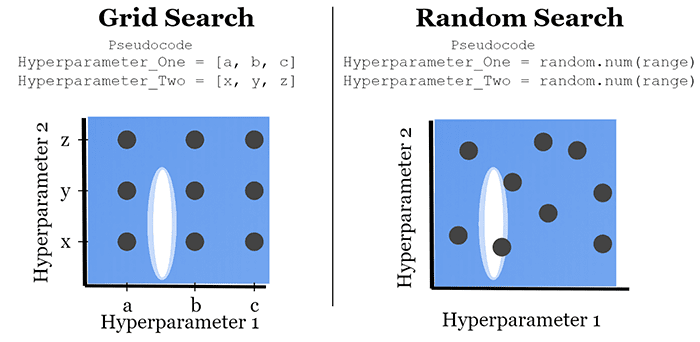
In Figure 2, we have a 2D grid with values of the first hyperparameter plotted along the x-axis and values of the second hyperparameter on the y-axis. The white highlighted oval is where the optimal values for both these hyperparameters lie. Our goal is to locate this region using our hyperparameter tuning algorithms.

Figure 2 (left) visualizes a grid search:

1. We start by defining a set of all hyperparameters and the associated values we want to explore
2. The grid search then examines all combinations of these hyperparameters
3. For each possible combination of hyperparameters, we train a model on them
4. The hyperparameters associated with the highest accuracy are then returned

A grid search is guaranteed to examine all possible combinations of hyperparameters. The problem is that the more hyperparameters you have, the more the number of combinations grows exponentially!

And since there are so many combinations to examine, a grid search tends to run very slowly.

To help speed the process, we can employ a random search (Figure 2, right).

With a random search, we:

1. Define the hyperparameters we want to search over
2. Set a lower and upper bound on the values (if it’s a continuous variable) or the possible values the hyperparameter can take on (if it’s a categorical variable) for each hyperparameter
3. A random search then randomly samples from these distributions a total of N times, training a model on each set of hyperparameters
4. The hyperparameters associated with the highest accuracy model are then returned

While a random search, by definition, is not an exhaustive search like the grid search, the benefit of a random search is that it’s far faster and typically obtains just as high accuracy as a grid search.

Why is that, though?

Shouldn’t a grid search obtain the highest accuracy since it’s so exhaustive?

Not necessarily.

When tuning hyperparameters, there isn’t just one “golden set of values” that will give you the highest accuracy. Instead, it’s a distribution — there are ranges for each hyperparameter that will obtain the best accuracy. If you land within that range/distribution, you’ll still enjoy the same high accuracy without the requirement of exhaustively tuning your hyperparameters with a grid search.

Configuring your development environment

To follow this guide, you need to have the scikit-learn machine library and Pandas data science library installed on your system.

Luckily, both of these packages are pip-installable:

$ pip install scikit-learn
$ pip install pandas

If you’re having a problem configuring your development environment, you should refer to the next section.

Having problems configuring your development environment?

All that said, are you:

• Short on time?
• Learning on your employer’s administratively locked system?
• Wanting to skip the hassle of fighting with the command line, package managers, and virtual environments?
• Ready to run the code right now on your Windows, macOS, or Linux systems?

Then join PyImageSearch University today!

Gain access to Jupyter Notebooks for this tutorial and other PyImageSearch guides that are pre-configured to run on Google Colab’s ecosystem right in your web browser! No installation required.

And best of all, these Jupyter Notebooks will run on Windows, macOS, and Linux!

Our example dataset

The dataset we’ll be using today is the Abalone from the UCI Machine Learning Repository.

Abalones are marine snails often studied by marine biologists. Specifically, marine biologists are interested in the age of the snail.

The problem is that determining the age of an abalone is a time consuming, tedious task, requiring the biologist to:

1. Cut the abalone shell through the cone
2. Stain it
3. Count the number of rings on the stained shell using a microscope (like measuring rings on a tree)

Yes, it’s just as boring as it sounds.

However, using more easily gathered values, it’s possible to predict the marine snail’s age.

The Abalone dataset includes seven values:

1. Length of the shell
2. Diameter of the shell
3. Height of the shell
4. Weight (entire weight of the abalone)
5. Shucked weight (weight of the abalone meat)
6. Viscera weight
7. Shell weight

Given these seven values, our goal is to train a machine learning model to predict the abalone’s age. As we’ll see, tuning hyperparameters to our machine learning model can lead to a boost in accuracy.

Project structure

Let’s start by reviewing our project directory structure.

Be sure to access the “Downloads” section of this tutorial to retrieve the source code.

You’ll then be presented with the following files:

$ tree . --dirsfirst
.
├── pyimagesearch
│   └── config.py
├── abalone_train.csv
├── train_svr.py
├── train_svr_grid.py
└── train_svr_random.py

1 directory, 5 files

The abalone_train.csv file contains the Abalone dataset from the UCI Machine Learning Repository (there is no need to download the CSV file from UCI as I have included the CSV file in the downloads associated with the tutorial).

The Abalone dataset contains 3,320 rows with eight columns per row (seven for the features, including shell length, diameter, etc.) and a final column for the age (which is the target value we seek to predict).

To evaluate the impact hyperparameter tuning has, we’ll be implementing three Python scripts:

1. train_svr.py: Establishes a baseline on the abalone dataset by training a Support Vector Regression (SVR) with no hyperparameter tuning.
2. train_svr_grid.py: Utilizes a grid search for hyperparameter tuning.
3. train_svr_random.py: Performs a random hyperparameter search over the distribution of hyperparameter values.

The config.py file inside the pyimagesearch module implements our important configuration variables used across the three driver scripts, including the path to the input CSV dataset and the column names.

Creating our configuration file

Before we can implement any training scripts, let’s first review our configuration file.

Open the config.py file in the pyimagesearch module, and you’ll find the following code:

# specify the path of our dataset
CSV_PATH = "abalone_train.csv"

# specify the column names of our dataframe
COLS = ["Length", "Diameter", "Height", "Whole weight",
	"Shucked weight", "Viscera weight", "Shell weight", "Age"]

On Line 2, we initialize the CSV_PATH to point to our Abalone CSV file residing on disk.

Lines 5 and 6 then define the names of each of the eight columns in the CSV file. We’ll need the column names in our training script to load it from disk and parse it.

That’s it for our configuration file! Let’s move on to implementing our training scripts.

Implementing a basic training script

Our first training script, train_svr.py, will establish a baseline accuracy by performing no hyperparameter tuning. Once we have this baseline, we’ll attempt to improve on it by applying hyperparameter tuning algorithms.

But for now, let’s establish our baseline.

Open the train_svr.py file in your project directory, and let’s get to work:

# import the necessary packages
from pyimagesearch import config
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.svm import SVR
import pandas as pd

Lines 2-6 import our required Python packages, including:

• config: The configuration file we implemented in the previous section
• StandardScaler: A data preprocessing technique that performs standard scaling (also known as z-scores in the statistics world) that scales each data observation by subtracting the mean of the particular column values divided by the standard deviation
• train_test_split: Constructs a training and testing split
• SVR: scikit-learn’s implementation of a Support Vector Machine used for regression
• pandas: Used to load our CSV file from disk and parse the data

Speaking of which, let’s load our Abalone CSV file from disk now:

# load the dataset, separate the features and labels, and perform a
# training and testing split using 85% of the data for training and
# 15% for evaluation
print("[INFO] loading data...")
dataset = pd.read_csv(config.CSV_PATH, names=config.COLS)
dataX = dataset[dataset.columns[:-1]]
dataY = dataset[dataset.columns[-1]]
(trainX, testX, trainY, testY) = train_test_split(dataX,
	dataY, random_state=3, test_size=0.15)

Line 12 reads our CSV file from disk. Notice how we pass in the CSV_PATH to the file on disk along with the names of the columns.

From there, we need to extract our feature vectors (i.e., length of the shell, diameter, height, etc.) and the target value we wish to predict (age) — Lines 13 and 14 do that for us via simple array slicing.

Once our data has been loaded and parsed, we construct a training and testing split on Lines 15 and 16 using 85% of the data for training and 15% for testing.

With our data loaded we now need to preprocess it:

# standardize the feature values by computing the mean, subtracting
# the mean from the data points, and then dividing by the standard
# deviation
scaler = StandardScaler()
trainX = scaler.fit_transform(trainX)
testX = scaler.transform(testX)

Line 21 instantiates an instance of our StandardScaler. We then compute the mean and standard deviation of all column values in our training data and then scale them (Line 22).

Line 23 scales our testing data using the mean and standard deviation computed over the training set.

All that’s left now is to train the SVR:

# train the model with *no* hyperparameter tuning
print("[INFO] training our support vector regression model")
model = SVR()
model.fit(trainX, trainY)

# evaluate our model using R^2-score (1.0 is the best value)
print("[INFO] evaluating...")
print("R2: {:.2f}".format(model.score(testX, testY)))

Line 27 instantiates our Support Vector Machine for regression. Remember, we are using regression here because we are trying to predict a real-valued output, the age of the abalone.

Line 28 then trains the model using our trainX (feature vectors) and trainY (target ages to predict).

Once our model is trained, we then evaluate it on Line 32 using the coefficient of determination.

The coefficient of determination is typically used when analyzing the output of a regression model. Essentially, it measures the amount of “explainable variance” between the dependent variable and the independent variable.

The coefficient will have a value in the range [0, 1], where 0 implies that we cannot predict the target output correctly, while a value of 1 implies we can perfectly predict the output with no error.

For more information on the coefficient of determination, be sure to refer to this page.

Gathering our baseline results (no hyperparameter tuning)

Before we can tune hyperparameters to our SVM, we first need to obtain a baseline with no hyperparameter tuning. Doing so will give us a baseline/benchmark where we can improve.

Start by accessing the “Downloads” section of this tutorial to retrieve the source code and example dataset.

You can then execute the train_svr.py script:

$ time python train_svr.py
[INFO] loading data...
[INFO] training our support vector regression model
[INFO] evaluating...
R2: 0.55

real	0m1.386s
user	0m1.928s
sys	0m1.040s

Here we obtain a coefficient of determination value of 0.55, meaning that 55% of the variance in Y (the age of the marine snails) is predictable based on X (our seven feature values).

Our goal is to use hyperparameter tuning to beat this value.

Tuning hyperparameters with a grid search

Now that we’ve established a baseline score, let’s see if we can beat it using hyperparameter tuning with scikit-learn.

We’ll start by implementing a grid search. Later in this guide, you’ll also learn how to use a random search for hyperparameter tuning as well.

Open the train_svr_grid.py file in your project directory structure, and we’ll implement a grid search using scikit-learn:

# import the necessary packages
from pyimagesearch import config
from sklearn.model_selection import RepeatedKFold
from sklearn.model_selection import GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVR
from sklearn.model_selection import train_test_split
import pandas as pd

Lines 2-8 import our required Python packages. These imports are identical to our previous train_svr.py script but with two additions:

1. GridSearchCV: scikit-learn’s implementation of the grid search hyperparameter tuning algorithm
2. RepeatedKFold: Performs k-fold cross-validation a total of N times using different randomization at each iteration

Performing k-fold cross-validation allows us to “improve the estimated performance of a machine learning model” (source) and is typically utilized when performing hyperparameter tuning.

The last thing you want when tuning hyperparameters is to run a long experiment on a randomized set of data, obtain high accuracy, and then find the high accuracy was due to an anomaly in the randomization of the data itself. Utilizing cross-validation helps prevent that from happening.

We can now load our CSV file from disk and preprocess it:

# load the dataset, separate the features and labels, and perform a
# training and testing split using 85% of the data for training and
# 15% for evaluation
print("[INFO] loading data...")
dataset = pd.read_csv(config.CSV_PATH, names=config.COLS)
dataX = dataset[dataset.columns[:-1]]
dataY = dataset[dataset.columns[-1]]
(trainX, testX, trainY, testY) = train_test_split(dataX,
	dataY, random_state=3, test_size=0.15)

# standardize the feature values by computing the mean, subtracting
# the mean from the data points, and then dividing by the standard
# deviation
scaler = StandardScaler()
trainX = scaler.fit_transform(trainX)
testX = scaler.transform(testX)

This code was covered in the “Implementing a basic training script” section above, so refer there if you need additional details on what the code is doing.

Next, we can initialize our regression model and hyperparameter search space:

# initialize model and define the space of the hyperparameters to
# perform the grid-search over
model = SVR()
kernel = ["linear", "rbf", "sigmoid", "poly"]
tolerance = [1e-3, 1e-4, 1e-5, 1e-6]
C = [1, 1.5, 2, 2.5, 3]
grid = dict(kernel=kernel, tol=tolerance, C=C)

Line 29 initializes our Support Vector Machine regression (SVR) model. An SVR has several hyperparameters to tune, including:

1. kernel: The type of kernel used when projecting the data into a higher-dimensional space where it ideally becomes linearly separable
2. tolerance: The tolerance for stopping criterion
3. C: The “strictness” of the SVR (i.e., to what degree the SVR is allowed to make mistakes when fitting the data)

Lines 30-32 define values for each of these hyperparameters, while Line 33 creates a dictionary of the hyperparameters.

Our goal will be to search these hyperparameters and find the optimal values for kernel, tolerance, and C.

Speaking of which, let’s perform our grid search now:

# initialize a cross-validation fold and perform a grid-search to
# tune the hyperparameters
print("[INFO] grid searching over the hyperparameters...")
cvFold = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
gridSearch = GridSearchCV(estimator=model, param_grid=grid, n_jobs=-1,
	cv=cvFold, scoring="neg_mean_squared_error")
searchResults = gridSearch.fit(trainX, trainY)

# extract the best model and evaluate it
print("[INFO] evaluating...")
bestModel = searchResults.best_estimator_
print("R2: {:.2f}".format(bestModel.score(testX, testY)))

Line 38 creates our cross-validation fold, indicating that we will generate 10 folds and then repeat the entire process a total of 3 times (typically, you’ll see fold and repeat values in the range [3, 10]).

Lines 39 and 40 instantiate our GridSearchCV object. Let’s break down each of the arguments:

• estimator: The model we’re attempting to optimize (i.e., our SVR that will predict the age of the abalone)
• param_grid: The hyperparameter search space
• n_jobs: The number of cores on your processor(s) that will be used to run parallel jobs. A value of -1 implies that all cores/processors will be used, thereby speeding the grid search process.
• scoring: The loss function we’re attempting to optimize; in this case, we are trying to drive down our mean squared error (MSE), implying that the lower the MSE, the better our model is at predicting the age of the abalone

Line 41 kicks off the grid search.

After the grid search runs, we obtain the bestModel found during the search (Line 45) and then compute the determination coefficient, which will tell us how good of a job our model did (Line 46).

Grid search hyperparameter tuning results

Let’s put the grid search hyperparameter tuning method to the test.

Be sure to access the “Downloads” section of this tutorial to retrieve the source code and example dataset.

From there, you can execute the following command:

$ time python train_svr_grid.py
[INFO] loading data...
[INFO] grid searching over the hyperparameters...
[INFO] evaluating...
R2: 0.56

real	4m34.825s
user	35m47.816s
sys	0m37.268s

Previously, no hyperparameter tuning yielded a coefficient of determination value of 0.55.

Using a grid search, we have improved that value to 0.56, implying that our tuned model is doing a better job predicting snail age.

However, obtaining this accuracy comes at the cost of speed:

• It only took 1.3 seconds to train our original model with no hyperparameter tuning
• An exhaustive grid search took 4m34s
• That’s an increase of 18,166%

And what’s worse is that the more hyperparameters you want to tune, the number of possible value combinations explodes exponentially — for real-world datasets and problems, that’s just not feasible.

The solution is to utilize a random search to tune your hyperparameters.

Tuning hyperparameters with a randomized search

Our final experiment will explore using a randomized hyperparameter search.

Open the train_svr_random.py file, and we’ll get started:

# import the necessary packages
from pyimagesearch import config
from sklearn.model_selection import RandomizedSearchCV
from sklearn.model_selection import RepeatedKFold
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVR
from sklearn.model_selection import train_test_split
from scipy.stats import loguniform
import pandas as pd

Lines 2-9 import our required Python packages. These imports are nearly identical to our previous two scripts, the most notable difference being RandomizedSearchCV, scikit-learn’s implementation of a randomized hyperparameter search.

With our imports taken care of we can load our abalone CSV file from disk and then preprocess it using the StandardScaler:

# load the dataset, separate the features and labels, and perform a
# training and testing split using 85% of the data for training and
# 15% for evaluation
print("[INFO] loading data...")
dataset = pd.read_csv(config.CSV_PATH, names=config.COLS)
dataX = dataset[dataset.columns[:-1]]
dataY = dataset[dataset.columns[-1]]
(trainX, testX, trainY, testY) = train_test_split(dataX,
	dataY, random_state=3, test_size=0.15)

# standardize the feature values by computing the mean, subtracting
# the mean from the data points, and then dividing by the standard
# deviation
scaler = StandardScaler()
trainX = scaler.fit_transform(trainX)
testX = scaler.transform(testX)

Next, we initialize our SVR model and then define the search space for our hyperparameters:

# initialize model and define the space of the hyperparameters to
# perform the randomized-search over
model = SVR()
kernel = ["linear", "rbf", "sigmoid", "poly"]
tolerance = loguniform(1e-6, 1e-3)
C = [1, 1.5, 2, 2.5, 3]
grid = dict(kernel=kernel, tol=tolerance, C=C)

From there we can tune the hyperparameters using a randomized search:

# initialize a cross-validation fold and perform a randomized-search
# to tune the hyperparameters
print("[INFO] grid searching over the hyperparameters...")
cvFold = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
randomSearch = RandomizedSearchCV(estimator=model, n_jobs=-1,
	cv=cvFold, param_distributions=grid,
	scoring="neg_mean_squared_error")
searchResults = randomSearch.fit(trainX, trainY)

# extract the best model and evaluate it
print("[INFO] evaluating...")
bestModel = searchResults.best_estimator_
print("R2: {:.2f}".format(bestModel.score(testX, testY)))

Lines 40-42 instantiate our RandomizedSearchCV object, similar to how we created our GridSearchCV tuner.

From there, Line 43 runs the randomized search over our hyperparameter space.

Finally, Lines 47 and 48 grab the best model found during the hyperparameter space and evaluate it on our testing set.

Randomized hyperparameter search results

We are now ready to see how our randomized hyperparameter search performs.

Access the “Downloads” section of this tutorial to retrieve the source code and Abalone dataset.

You can then execute the train_svr_random.py script.

$ time python train_svr_random.py
[INFO] loading data...
[INFO] grid searching over the hyperparameters...
[INFO] evaluating...
R2: 0.56

real	0m36.771s
user	4m36.760s
sys	0m6.132s

Here, we obtain a coefficient of determination value of 0.56 (the same as our grid search); however, the random search took only 36 seconds instead of the grid search, which took 4m34s.

Whenever possible, I suggest you use a randomized search instead of a grid search for hyperparameter tuning. You’ll typically obtain a similar accuracy in a fraction of the time.

Summary

In this tutorial, you learned the basics of hyperparameter tuning using scikit-learn and Python.

We investigated hyperparameter tuning by:

1. Obtaining a baseline accuracy on our dataset with no hyperparameter tuning — this value became our score to beat
2. Utilizing an exhaustive grid search
3. Applying a randomized search

Both the grid search and random search beat the original baseline, but the random search did so in 86% less time.

I suggest using randomized searches when tuning your hyperparameters, as the time savings alone make it more practical and useful in machine learning projects.

To download the source code to this post (and be notified when future tutorials are published here on PyImageSearch), simply enter your email address in the form below!